题目内容
 如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接BC,AD.
如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接BC,AD.
(1)在图中找出与∠BAC相等的角,并说明理由;
(2)在图中找出所有与△BCE相似的三角形:______;(不必证明)
(3)若BE=4,ED=5,求BC的长.
解:(1)∵AB=BC,
∴ =
= ,
,
∴∠BAC=∠BCA=∠BDC=∠BDA;
(2)由圆周角定理可知∠CBD=∠CAD,
又∵∠BCA=∠BDC=∠BDA,
∴△BCE∽△BDC∽△ADE;
故答案为:△BCE∽△BDC∽△ADE;
(3)由已知得BD=BE+ED=9,
∵△BCE∽△BDC,
∴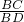 =
= ,即
,即 =
=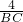 ,
,
解得BC=6.
分析:(1)根据等腰三角形的性质,圆周角定理,可找出与∠BAC相等的角;
(2)由圆周角定理及(1)中相等的角,利用“AA”确定相似三角形;
(3)由(2)可知△BCE∽△BDC,结合已知条件,确定相似比为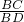 =
= ,利用这个等式求BC.
,利用这个等式求BC.
点评:本题考查了圆周角定理,相似三角形的判定与性质.关键是由已知条件得出弧相等,由圆周角定理得出圆周角相等.
∴
 =
= ,
,∴∠BAC=∠BCA=∠BDC=∠BDA;
(2)由圆周角定理可知∠CBD=∠CAD,
又∵∠BCA=∠BDC=∠BDA,
∴△BCE∽△BDC∽△ADE;
故答案为:△BCE∽△BDC∽△ADE;
(3)由已知得BD=BE+ED=9,
∵△BCE∽△BDC,
∴
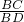 =
= ,即
,即 =
=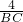 ,
,解得BC=6.
分析:(1)根据等腰三角形的性质,圆周角定理,可找出与∠BAC相等的角;
(2)由圆周角定理及(1)中相等的角,利用“AA”确定相似三角形;
(3)由(2)可知△BCE∽△BDC,结合已知条件,确定相似比为
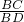 =
= ,利用这个等式求BC.
,利用这个等式求BC.点评:本题考查了圆周角定理,相似三角形的判定与性质.关键是由已知条件得出弧相等,由圆周角定理得出圆周角相等.

练习册系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=