题目内容
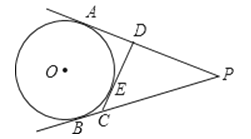
【题目】在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为( )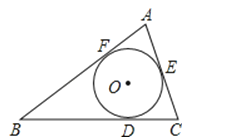
A.AF=4,BD=9,CE=5
B.AF=4,BD=5,CE=9
C.AF=5,BD=4,CE=9
D.AF=9,BD=4,CE=5
【答案】A
【解析】解:设AF=xcm,BD=ycm,CE=zcm.
∵AF、AE是圆的切线,
∴AE=AF=xcm,
同理:BF=BD=ycm,CD=CE=zcm.
根据题意得: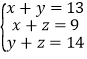 ,
,
解得:![]() .
.
即:AF=4,BD=9,CE=5.
故选A.
【考点精析】认真审题,首先需要了解三角形的内切圆与内心(三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心).

练习册系列答案
相关题目