题目内容
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )

A. 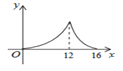 B.
B. 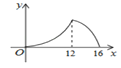 C.
C. 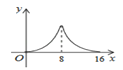 D.
D. 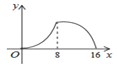
【答案】B
【解析】分点Q在AC上和BC上两种情况进行讨论即可.
解:当点Q在AC上时,
∵∠A=30°,AP=x,
∴PQ=xtan30°= ![]()
∴y=![]() ×AP×PQ=
×AP×PQ=![]() ×x×
×x×![]() =
=![]() ;
;
当点Q在BC上时,如下图所示:

∵AP=x,AB=16,∠A=30°,
∴BP=16-x,∠B=60°,
∴PQ=BPtan60°=![]() (16-x).
(16-x).
∴S△APQ=![]() APPQ=
APPQ=![]() x
x![]() (16-x)=
(16-x)=![]() x2+8
x2+8![]() x.
x.
∴该函数图象前半部分是抛物线开口向上,后半部分也为抛物线开口向下.
故选B.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目