Question

【题目】在平面直角坐标系中，抛物线y=x2﹣6mx+5与y轴的交点为A，与x轴的正半轴分别交于点B（b，0），C（c，0）．
（1）当b=1时，求抛物线相应的函数表达式；
（2）当b=1时，如图，E（t，0）是线段BC上的一动点，过点E作平行于y轴的直线l与抛物线的交点为P．求△APC面积的最大值；

（3）当c=b+n时，且n为正整数，线段BC（包括端点）上有且只有五个点的横坐标是整数，求b的值．

Answer 1

【答案】
（1）

解：当b=1时，将点B（1，0）代入抛物线y=x2﹣6mx+5中，得m=1，

∴y=x2﹣6x+5

（2）

解：如图1中，直线AC与PE交于点F．

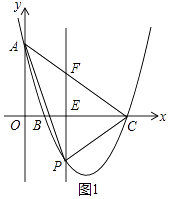
当b=1时，求得A（0，5），B（1，0），C（5，0），可得AC所在的一次函数表达式为y=﹣x+5，

∵E（t，0），

∴P （t，t2﹣6t+5），直线l与AC的交点为F（t，﹣t+5），

∴PF=（﹣t+5）﹣（t2﹣6t+5）=﹣t2+5t，

∴S△APC= ×（﹣t2+5t）5=﹣ （t﹣ ）2+ ，

∵﹣ ＜0，

∴当t= 时，面积S有最大值

（3）

解：①当b整数时，n为整数，

∴n=4，c=b+4．则b，b+4是方程x2﹣mx+5=0的两个根，分别代入方程中，

得b2﹣mb+5=0 ①，（b+4）2﹣m（b+4）+5=0 ②，

由①②可得b2+4b﹣5=0，解得b=1或﹣5（舍）；

或由一元二次方程根与系数的关系得 b（b+4）=5解得b=1或﹣5（舍）．

②当b小数时，n为整数，∴n=5，c=b+5为小数，则b，b+5是方程x2﹣mx+5=0的两个根，同样可得b= 或 （舍弃）；

∴b=1或

【解析】（1）当b=1时，将点B（1，0）代入抛物线y=x2﹣6mx+5中求出m，即可解决问题．（2）如图1中，直线AC与PE交于点F．切线直线AC的解析式，构建二次函数，利用二次函数的性质即可解决问题．（3）分两种情形①当b整数时，n为整数，可知n=4，c=b+4．则b，b+4是方程x2﹣mx+5=0的两个根，分别代入方程中求解即可，②当b小数时，n为整数，∴n=5，c=b+5为小数，则b，b+5是方程x2﹣6x+5=0的两个根，
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．