题目内容
【题目】如图,海上救援船要从距离海岸8海里的![]() 点位置到海岸
点位置到海岸![]() 的
的![]() 处携带救援设备,然后到距离海岸16海里处的
处携带救援设备,然后到距离海岸16海里处的![]() 点处对故障船实施救援.已知
点处对故障船实施救援.已知![]() 间的距离为18海里,为使救援船尽快赶到故障船实施救援,救援设备被放置在恰当位置.
间的距离为18海里,为使救援船尽快赶到故障船实施救援,救援设备被放置在恰当位置.
(1)试在图中确定点![]() 的位置;
的位置;
(2)若救援船的速度是20节(1节=1海里/小时),求这艘救援船最快多长时间到达故障船?
【答案】(1)见解析;(2)1.5
【解析】
(1)利用“直线同侧两点到直线上一点距离的和最短的问题”模型,利用轴对称的知识,确定M的位置.
(2)补全图形,利用勾股定理,得到EC的长,从而得到到达所用时间.
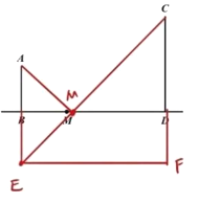
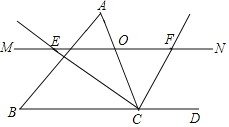
解:(1)延长AB至E,使BE=AB,连接EC交BD于M,连接AM,则点M即为所求.
(2)依题意有AB=8,CD=16,BD=18,
根据(1)的作图可知,点A,E关于直线BD对称,
∴AB=BE=8,AM=EM,
过点E作EF![]() BD,交CD的延长线与F,
BD,交CD的延长线与F,
∵四边形BEFD为矩形,
∴EF=BD=18,AB=BE=DF=8,
∴CF=CD+DF=16+8=24,
在![]() ECF中,
ECF中,![]() ,
,
∴AM+MC=EM+MC=EC=30,
又∵救援船的速度是20节,即为20×1=20(海里/小时),
∵![]() (小时).
(小时).
∴这艘救援船最快到达故障船的时间为1.5小时.

练习册系列答案
相关题目