题目内容
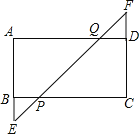
【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=![]() ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
【答案】(1)证明见解析;(2)8.
【解析】试题分析:
(1)由矩形的性质得出∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,证出∠E=∠F,AE=CF,由ASA证明△CFP≌△AEQ,即可得出结论;(2)证明△BEP、△AEQ是等腰直角三角形,得出BE=BP=1,AQ=AE,求出PE=![]() ,得出EQ=PE+PQ=
,得出EQ=PE+PQ=![]() ,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE-BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD的面积;
,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE-BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD的面积;
试题解析:
(1)证明:
∵四边形ABCD是矩形
∴∠A=∠ABC=∠C=∠ADC=90°
∴AB=CD,AD=BC,AB∥CD,AD∥BC
∴∠E=∠F
∵BE=DF
∴AE=CF
在△CFP和△AEQ中
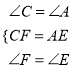
∴△CFP≌△AEQ(ASA)
∴CP=AQ
(2)解:∵AD∥BC
∴∠PBE=∠A=90°
∵∠AEF=45°
∴△BEP、△AEQ是等腰直角三角形
∴BE=BP=1,AQ=AE
∴PE=![]() BP=
BP=![]()
∴EQ=PE+PQ=![]() +2
+2![]() =3
=3![]()
∴AQ=AE=3
∴AB=AE﹣BE=2
∵CP=AQ,AD=BC
∴DQ=BP=1
∴AD=AQ+DQ=3+1=4
∴矩形ABCD的面积=AB×AD=2×4=8.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目