Question

如图，F为正方形ABCD的对角线AC上一点，FE⊥AD于点E，M为CF的中点．
（1）求证：MB=MD；
（2）求证：ME=MB．

Answer 1

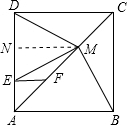证明：（1）∵四边形ABCD是正方形，
∴BC=DC，∠BCM=∠DCM，
又MC=MC，∴△BCM≌△DCM，
∴MB=MD；

（2）在直角梯形DEFC中，CD∥FE，
取DE的中点N，连接MN，
∵M为CF的中点，∴MN∥CD，
又CD⊥DE，∴MN⊥DE，
∴MN是线段DE的垂直平分线，
∴MD=ME，
由（1）知，MB=MD，∴ME=MB．
分析：（1）根据正方形的性质及SAS定理可直接求出△BCM≌△DCM，利用全等三角形的性质求解即可；
（2）取DE的中点N，连接MN，根据梯形的中位线定理可求出MN∥CD，MN⊥DE，可求出MN是线段DE的垂直平分线，即△DEM是等腰三角形，由等腰三角形的性质即可解答．
点评：此题比较简单，考查的是正方形的性质及等腰三角形的判定定理，解答此题的关键是根据题意作出辅助线，构造出直角梯形的中位线求解．