题目内容
先阅读,再解题.
解不等式: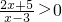
解:根据两数相除,同号得正,异味号得负,得
① 或②
或②
解不等式组①,得x>3
解不等式组②,得x<-
所以原不等式的解集为x>3或x<- .
.
参照以上解题过程所反映的解题思想方法,试解不等式: .
.
解:根据两数相除,同号得正,异号得负,得
①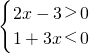 或②
或②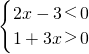 ,
,
不等式组①得不等式组无解,
解不等式组②,得- <x<
<x< ,
,
所以原不等式的解集为- <x<
<x< .
.
分析:利用有理数除法性质得到①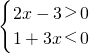 或②
或②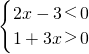 ,再分别解两个不等式组得到①无解,②的解集为-
,再分别解两个不等式组得到①无解,②的解集为-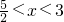 ,然后确定原不等式的解集.
,然后确定原不等式的解集.
点评:本题考查了解一元一次不等式组:分别求出不等式组各不等式的解集,然后根据“同大取大,同小取小,大于小的小于大的取中间,大于大的小于小的无解”确定不等式组的解集.也考查了阅读理解能力.
①
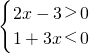 或②
或②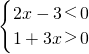 ,
,不等式组①得不等式组无解,
解不等式组②,得-
 <x<
<x< ,
,所以原不等式的解集为-
 <x<
<x< .
.分析:利用有理数除法性质得到①
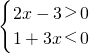 或②
或②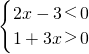 ,再分别解两个不等式组得到①无解,②的解集为-
,再分别解两个不等式组得到①无解,②的解集为-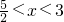 ,然后确定原不等式的解集.
,然后确定原不等式的解集.点评:本题考查了解一元一次不等式组:分别求出不等式组各不等式的解集,然后根据“同大取大,同小取小,大于小的小于大的取中间,大于大的小于小的无解”确定不等式组的解集.也考查了阅读理解能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 (a≠0)如下:
(a≠0)如下: ,
, .
. ,得
,得 ,即
,即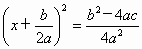 .
.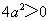 ,从而当
,从而当 时,方程右边是一个正数,正数的平方根有两个,因此方程有两个不相等的实数根;当
时,方程右边是一个正数,正数的平方根有两个,因此方程有两个不相等的实数根;当 时,方程右边是零,因此方程有两个相等的实数根;当
时,方程右边是零,因此方程有两个相等的实数根;当 时,方程右边是一个负数,而负数没有平方根,因此方程没有实数根.所以我们可以根据
时,方程右边是一个负数,而负数没有平方根,因此方程没有实数根.所以我们可以根据 的值来判断方程的根的情况,请利用上述论断,不解方程,判别方程
的值来判断方程的根的情况,请利用上述论断,不解方程,判别方程 的根的情况.
的根的情况.
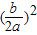 ,得
,得 ,即
,即