��Ŀ����
���Ķ����ٽ���
���䷽����һԪ���η���ax2+bx+c=0��a��0�����£�
�����ax2+bx=-c��
�������߳���a����x2+
x=-
����������(
)2����x2+
x+(
)2=-
+(
)2����(x+
)2=
��Ϊa��0������4a2��0���Ӷ���b2-4ac��0ʱ�������ұ���һ��������������ƽ��������������˷�������������ȵ�ʵ��������b2-4ac=0ʱ�������ұ����㣬��˷�����������ȵ�ʵ��������b2-4ac��0ʱ�������ұ���һ��������������û��ƽ��������˷���û��ʵ������
�������ǿ��Ը���b2-4ac��ֵ���жϷ��̵ĸ�������������������۶ϣ����ⷽ�̣��б����з��̵ĸ��������
��1��x2-14x+12=0 ��2��4x2+12x+9=0 ��3��2x2-3x+6=0 ��4��3x2+3x-4=0��
���䷽����һԪ���η���ax2+bx+c=0��a��0�����£�
�����ax2+bx=-c��
�������߳���a����x2+
| b |
| a |
| c |
| a |
����������(
| b |
| 2a |
| b |
| a |
| b |
| 2a |
| c |
| a |
| b |
| 2a |
| b |
| 2a |
| b2-4ac |
| 4a |
��Ϊa��0������4a2��0���Ӷ���b2-4ac��0ʱ�������ұ���һ��������������ƽ��������������˷�������������ȵ�ʵ��������b2-4ac=0ʱ�������ұ����㣬��˷�����������ȵ�ʵ��������b2-4ac��0ʱ�������ұ���һ��������������û��ƽ��������˷���û��ʵ������
�������ǿ��Ը���b2-4ac��ֵ���жϷ��̵ĸ�������������������۶ϣ����ⷽ�̣��б����з��̵ĸ��������
��1��x2-14x+12=0 ��2��4x2+12x+9=0 ��3��2x2-3x+6=0 ��4��3x2+3x-4=0��
��1����Ϊb2-4ac=��-14��2-4��12=148��0�����ԣ�ԭ��������������ȵ�ʵ����
��2����Ϊb2-4ac=122-4��4��9=0��
���ԣ�ԭ������������ȵ�ʵ����
��3����Ϊb2-4ac=��-3��2-4��2��6=-39��0��
���ԣ�ԭ������ʵ����
��4����Ϊb2-4ac=9+4��3��4=57��0�����ԣ�ԭ��������������ȵ�ʵ����
��2����Ϊb2-4ac=122-4��4��9=0��
���ԣ�ԭ������������ȵ�ʵ����
��3����Ϊb2-4ac=��-3��2-4��2��6=-39��0��
���ԣ�ԭ������ʵ����
��4����Ϊb2-4ac=9+4��3��4=57��0�����ԣ�ԭ��������������ȵ�ʵ����

��ϰ��ϵ�д�
�����Ŀ
 (a��0)���£�
(a��0)���£� ��
�� ��
�� ����
���� ����
����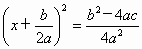 ��
��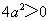 ���Ӷ���
���Ӷ��� ʱ�������ұ���һ��������������ƽ��������������˷�������������ȵ�ʵ��������
ʱ�������ұ���һ��������������ƽ��������������˷�������������ȵ�ʵ�������� ʱ�������ұ����㣬��˷�����������ȵ�ʵ��������
ʱ�������ұ����㣬��˷�����������ȵ�ʵ�������� ʱ�������ұ���һ��������������û��ƽ��������˷���û��ʵ�������������ǿ��Ը���
ʱ�������ұ���һ��������������û��ƽ��������˷���û��ʵ�������������ǿ��Ը��� ��ֵ���жϷ��̵ĸ�������������������۶ϣ����ⷽ�̣��б�
��ֵ���жϷ��̵ĸ�������������������۶ϣ����ⷽ�̣��б� �ĸ��������
�ĸ��������
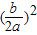 ����
���� ����
����