题目内容
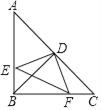
【题目】如图，在△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE，点E在BC上．过点D作DF∥BC，连接DB．
求证：（1）△ABD≌△ACE；
（2）DF=CE．
【答案】（1）证明见解析；（2）证明见解析.
【解析】
（1）求出∠BAD=∠BAC，根据SAS证出△BAD≌△CAE即可；
（2）根据全等推出∠DBA=∠C，根据等腰三角形性质得出∠C=∠ABC，根据平行线性质得出∠ABC=∠DFB，推出∠DFB=∠DBF，根据等腰三角形的判定推出即可．
（1）∵∠BAC=∠DAE，∴∠BAC﹣∠BAE=∠DAE﹣∠BAE，∴∠BAD=∠EAC．在△BAD和△CAE中，∵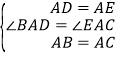
，∴△BAD≌△CAE（SAS）；
（2）∵△BAD≌△CAE，∴∠DBA=∠C．
∵AB=AC，∴∠C=∠ABC．
∵DF∥BC，∴∠DFB=∠ABC=∠C=∠DBA，即∠DFB=∠DBF，∴DF=CE．
练习册系列答案
名校课堂系列答案
相关题目
