题目内容
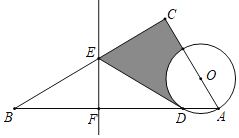
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若∠B=30°,AC=6,OA=2,直接写出阴影部分的面积.
【答案】(1)直线DE与⊙O相切;理由见解析;(2)![]() .
.
【解析】
(1)直线DE与⊙O相切,连接OD,由已知条件证明OD⊥DE即可证明DE是⊙O的切线;
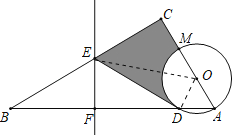
(2)连接OE,根据阴影部分的面积=四边形CEDO-扇形DOM的面积计算即可.
(1)直线DE与⊙O相切,理由如下:
连接OD,
∵OD=OA,
∴∠A=∠ODA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°﹣90°=90°,
即OD⊥DE,
又∵OD为⊙O的半径,
∴直线DE与⊙O相切;
(2)连接OE,
∵∠B=30°,
∴∠A=60°,
∵OD=OA,
∴∠ODA=∠A=60°,
∴AD=AO=DO=2,∠MOD=120°,
∵AC=6,∠B=30°,
∴AB=12,
∴BD=10,
∵EF是BD的垂直平分线,
∴BF=DF=5,
∴EF=![]() ,BE=DE=
,BE=DE=![]() ,
,
∴CE=BC﹣BE=![]() ,
,
∴阴影部分的面积=四边形CEDO﹣扇形DOM的面积=![]() ×
×![]() ×4+
×4+![]() ×
×![]() ×2﹣
×2﹣![]() =
=![]() .
.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目