题目内容
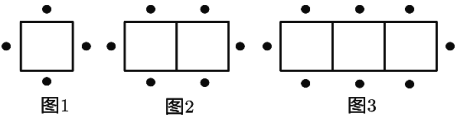
【题目】一张正方形桌子可坐4人，按图1—图3的方式将桌子拼在一起并安排人员就坐．
（1）两张桌子拼在一起可做 人，三张桌子拼在一起可坐 人，
张桌子拼在一起可坐 人
（2）一家酒楼有60张这样的桌子，按照图1—图3方式每4张拼成一个大桌子，则60张桌子可拼成15张大桌子，共可坐 人
（3）在问题（2）中，若每4张桌子拼成一个大的正方形桌子，则可坐 人
【答案】（1）
，
， 
；（2）150；（3）120
【解析】
(1)观察摆放的桌子，不难发现；在1张桌子坐4人的基础上，多一张桌子多2个人，从而推出n张桌子时，有4+2（n-1）=2n+2，代入即可求解；
(2)先利用(1)题得出的规律算出一张大桌子能坐10个人，则15张大桌子可以坐15×10=150人；
(3)4张桌子拼成一个大正方形的桌子时可以坐8个人，15×8=120人.
解：(1)4+2=6，6+2=8，4+2（n-1）=2n+2；
(2)(2×4+2)×15=150（人）
(3)2×4×15=120（人）
练习册系列答案
相关题目
【题目】某中学开展“唱红歌”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示．
班级 | 平均数（分） | 中位数 | 众数 |
九（1） | 85 | 85 | |
九（2） | 80 |
（1）根据图示填写上表；
（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；
（3）计算两班复赛成绩的方差，并说明哪个班级的成绩较稳定.
