题目内容
(2013•台州二模)(1)计算:2sin60°-
+(
)-1
(2)解方程:x2+4x+1=0.
| ||
| 3 |
| 1 |
| 3 |
(2)解方程:x2+4x+1=0.
分析:(1)先计算特殊角的三角形函数值、化简二次根式,负整数指数幂;然后根据实数运算法则进行计算;
(2)把常数项1移项后,应该在左右两边同时加上一次项系数4的一半的平方.
(2)把常数项1移项后,应该在左右两边同时加上一次项系数4的一半的平方.
解答:解:(1)原式=2×
-
+3,
=
-
+3,
=3;
(2)移项,得
x2+4x=-1.
配方,得
x2+4x+22=-1+22,
即(x+1)2=3,
开方得:x+1=±
,
∴x1=-1+
,x2=-1-
.
| ||
| 2 |
3
| ||
| 3 |
=
| 3 |
| 3 |
=3;
(2)移项,得
x2+4x=-1.
配方,得
x2+4x+22=-1+22,
即(x+1)2=3,
开方得:x+1=±
| 3 |
∴x1=-1+
| 3 |
| 3 |
点评:本题考查了解一元二次方程--配方法,实数的运算以及特殊角的三角函数值等.用配方法解一元二次方程的步骤:
(1)形如x2+px+q=0型:第一步移项,把常数项移到右边;第二步配方,左右两边加上一次项系数一半的平方;第三步左边写成完全平方式;第四步,直接开方即可.
(2)形如ax2+bx+c=0型,方程两边同时除以二次项系数,即化成x2+px+q=0,然后配方.
(1)形如x2+px+q=0型:第一步移项,把常数项移到右边;第二步配方,左右两边加上一次项系数一半的平方;第三步左边写成完全平方式;第四步,直接开方即可.
(2)形如ax2+bx+c=0型,方程两边同时除以二次项系数,即化成x2+px+q=0,然后配方.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
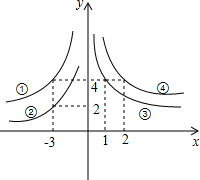 (2013•台州二模)如图,双曲线y=-
(2013•台州二模)如图,双曲线y=- →y=3
→y=3 +1;y=3
+1;y=3 →y=3
→y=3 +1;y=
+1;y= →y=
→y= +1;…
+1;… +1图象再往 平移 个单位,所得函数图象的解析式为y=
+1图象再往 平移 个单位,所得函数图象的解析式为y= +1;
+1; +1图象性质的描述:
+1图象性质的描述: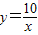 的图象的一部分,滑道BCD是二次函数图象的一部分,两滑道的连接点B为抛物线的顶点,且B点到地面的距离为2米,当甲同学滑到C点时,距地面的距离为1米,距点B的水平距离CE也为1米.
的图象的一部分,滑道BCD是二次函数图象的一部分,两滑道的连接点B为抛物线的顶点,且B点到地面的距离为2米,当甲同学滑到C点时,距地面的距离为1米,距点B的水平距离CE也为1米.