题目内容
【题目】整式乘法和乘法公式
(1)计算:(﹣x)2(2y)3
(2)化简:(a+1)2+2(a﹣1)(a+1)+(a﹣1)2
(3)如果(x+1)(x2+ax+b)的乘积中不含x2项和x项,求下面式子的值:(a+2b)(a+b)﹣2(a+b)2
(4)课本上,公式(a﹣b)2=a2﹣2ab+b2是由公式(a+b)2=a2+2ab+b2推导得出的,已知(a+b)3=a3+3a2b+3ab2+b3,则(a﹣b)3= .
【答案】(1)8x2y3;(2)4a2;(3)0;(4)a3﹣3a2b+3ab2﹣b3.
【解析】
(1)根据幂的乘方与积的乘方即可解答本题;
(2)根据完全平方公式和平方差公式即可解答本题;
(3)根据(x+1)(x2+ax+b)的乘积中不含x2项和x项,可以求得a、b的值,从而可以求得所求式子的值;
(4)根据(a+b)3=a3+3a2b+3ab2+b3,可以求得所求式子的结果.
(1)(﹣x)2(2y)3
=x28y3
=8x2y3;
(2)(a+1)2+2(a﹣1)(a+1)+(a﹣1)2
=a2+2a+1+2(a2﹣1)+a2﹣2a+1
=a2+2a+1+2a2﹣2+a2﹣2a+1
=4a2;
(3)(x+1)(x2+ax+b)
=x3+ax2+bx+x2+ax+b
=x3+(a+1)x2+(a+b)x+b,
∵(x+1)(x2+ax+b)的乘积中不含x2项和x项,
∴![]() ,得
,得![]() ,
,
当a=﹣1,b=1时,
(a+2b)(a+b)﹣2(a+b)2
=(﹣1+2×1)(﹣1+1)﹣2(﹣1+1)2
=1×0﹣2×02
=0﹣0
=0;
(4)∵(a+b)3=a3+3a2b+3ab2+b3,
∴[a+(﹣c)]3=a3+3a2(﹣c)+3a(﹣c)2+(﹣c)3=a3﹣3a2c+3ac2﹣c3,
∴(a﹣b)3=a3﹣3a2b+3ab2﹣b3,
故答案为:a3﹣3a2b+3ab2﹣b3.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验,每人打10发子弹.下表是甲、乙两人各自的射击情况记录(其中乙的记录表上射中9,10环的子弹数被墨水污染看不清楚,但是教练记得乙射中9,10环的子弹数均不为0发).
甲
中靶环数(环) | 5 | 6 | 8 | 9 | 10 |
射中此环的子弹数(发) | 4 | 1 | 3 | 1 | 1 |
乙
中靶环数(环) | 5 | 6 | 7 | 9 | 10 |
射中此环的子弹数(发) | 2 | 3 | 2 |
(1)求甲同学在这次测验中平均每次射中的环数;
(2)从这次测验的平均成绩的角度考虑,如果你是教练,你认为选谁参加比赛比较合适?并说明理由.
【题目】某班进行了一次数学測验,将成绩绘制成频数分布表和频数直方图的一部分如下:
成绩 | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
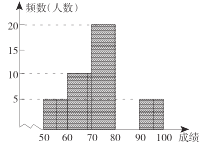
(1)在频数分布表中,![]() 的值为________,
的值为________,![]() 的值为________;
的值为________;
(2)将频数直方图补充完整;
(3)成绩在![]() 分以上(含
分以上(含![]() )的学生人数占全班总人数的百分比是多少?
)的学生人数占全班总人数的百分比是多少?