题目内容
【题目】下列命题中,说法正确的个数是( )
(1)两个等边三角形一定相似;(2)有一个角相等的两个菱形一定相似;
(3)两个等腰三角形腰上的高和腰对应成比例,则这两个三角形必相似;
(4)两边及第三边上的中线对应成比例的两三角形相似.
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
利用相似图形的判定和性质,分别判断即可.
解:(1)等边三角形的内角都是60°,各边相等,得到对应边的比相等.所以一定相似,正确;
(2)有一个角相等的两个菱形,其余的角也必对应相等,菱形各边相等,所以对应边的比相等,所以一定相似,正确;
(3)根据斜边和一条直角边对应成比例的两个直角三角形相似,可得这两个等腰三角形的顶角相等,然后由腰对应成比例可得这两个三角形必相似,正确;
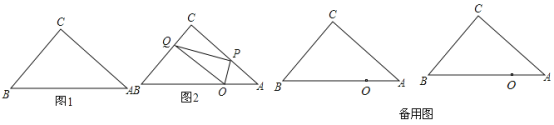
(4)理由:如图,AD、A′D′分别是△ABC与△A′B′C′的中线,![]() ,
,
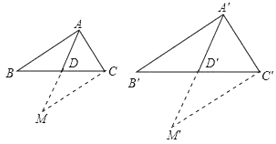
延长AD到M,使DM=AD,连结MC.
在△ABD与△MCD中,AD=MD,∠ADB=∠MDC,BD=CD,
∴△ABD≌△MCD(SAS),
∴AB=MC,
同理延长A′D′到M′,使D′M′=A′D′,连结M′C′,那么A′B′=M′C′,
∴![]() ,
,
在△ACM与△A′C′M′中,![]() ,
,
∴△ACM∽△A′C′M′,
∴∠MAC=∠M′A′C′,
同理可得∠MAB=∠M′A′B′,
∴∠MAC+∠MAB=∠M′A′C′+∠M′A′B′,即∠BAC=∠B′A′C′.
在△ABC与△A′B′C′中,![]() ,∠BAC=∠B′A′C′,
,∠BAC=∠B′A′C′,
∴△ABC∽△A′B′C′,
∴两边及第三边上的中线对应成比例的两三角形相似,正确.
故选:D.

练习册系列答案
相关题目