题目内容
已知x.y是实数,且满足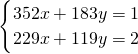 ,则x+y=________
,则x+y=________
-12
分析:由于方程组中未知数的系数较大且同一未知数的两个系数都互质,所以不管用代入法还是加减法分别求出x与y的值,计算量都很大.考虑运用整体思想解这个方程组.又因为题目要求x+y的值,所以把x+y当作一个整体,将原方程组变形为 ,此方程组中的两个未知数分别是x与x+y,运用加减法消去未知数x即可.
,此方程组中的两个未知数分别是x与x+y,运用加减法消去未知数x即可.
解答:原方程组可写成 ,
,
①×110-②×169,得19(x+y)=-228,
解得 x+y=-12.
故答案为-12.
点评:本题考查了二元一次方程组的解法,属于基础题型,但由于未知数的系数特点,难度较大.解二元一次方程组主要是通过消元(代入消元法、加减消元法),化二元一次方程组为一元一次方程,然后求出二元一次方程组的解.本题通过整体思想的运用,提高了解题速度和准确性.
分析:由于方程组中未知数的系数较大且同一未知数的两个系数都互质,所以不管用代入法还是加减法分别求出x与y的值,计算量都很大.考虑运用整体思想解这个方程组.又因为题目要求x+y的值,所以把x+y当作一个整体,将原方程组变形为
 ,此方程组中的两个未知数分别是x与x+y,运用加减法消去未知数x即可.
,此方程组中的两个未知数分别是x与x+y,运用加减法消去未知数x即可.解答:原方程组可写成
 ,
,①×110-②×169,得19(x+y)=-228,
解得 x+y=-12.
故答案为-12.
点评:本题考查了二元一次方程组的解法,属于基础题型,但由于未知数的系数特点,难度较大.解二元一次方程组主要是通过消元(代入消元法、加减消元法),化二元一次方程组为一元一次方程,然后求出二元一次方程组的解.本题通过整体思想的运用,提高了解题速度和准确性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知m,n是实数,且满足m2+2n2+m-
n+
=0,则-mn2的平方根是( )
| 4 |
| 3 |
| 17 |
| 36 |
A、
| ||||
B、±
| ||||
C、
| ||||
D、±
|