题目内容
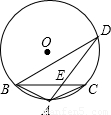
(2008•清远)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F在BD上,且BE=DF.(1)求证:△ABE≌△CDF;
(2)在不添加辅助线的情况下,请你补充一个条件,使得四边形AECF是菱形,并给予证明.

【答案】分析:1、由平行四边形的性质知,AB=CD,AB∥CD,得到∠ABE=∠CDF,又有BE=DF,故由SAS证得△ABE≌△CDF.
2、平行四边形的性质知,AO=CO,BO=DO,由BE=DF可求得OE=OF,则四边形AECF是平行四边形,若使平行四边形AECF为菱形,只要AC⊥EF即可.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.(1分)
∴∠ABE=∠CDF.
又∵BE=DF,(3分)
∴△ABE≌△CDF.(4分)
(2)解:补充的条件是:AC⊥BD.
证明:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,
∴0E=0F.
∴四边形AECF是平行四边形.(5分)
又∵AC⊥BD,
∴四边形AECF是菱形.(6分)
(其他解法参照给分)
点评:本题利用了平行四边形的判定和性质,全等三角形和菱形的判定求解.
2、平行四边形的性质知,AO=CO,BO=DO,由BE=DF可求得OE=OF,则四边形AECF是平行四边形,若使平行四边形AECF为菱形,只要AC⊥EF即可.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.(1分)
∴∠ABE=∠CDF.
又∵BE=DF,(3分)
∴△ABE≌△CDF.(4分)
(2)解:补充的条件是:AC⊥BD.
证明:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,
∴0E=0F.
∴四边形AECF是平行四边形.(5分)
又∵AC⊥BD,
∴四边形AECF是菱形.(6分)
(其他解法参照给分)
点评:本题利用了平行四边形的判定和性质,全等三角形和菱形的判定求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
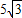 米,若挖掘的速度为2米/小时,几小时后到达B点?
米,若挖掘的速度为2米/小时,几小时后到达B点?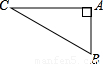
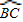 的中点,AD交BC于点E,AE=4,AB=6,求DE的长.
的中点,AD交BC于点E,AE=4,AB=6,求DE的长.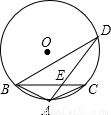
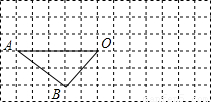
 的中点,AD交BC于点E,AE=4,AB=6,求DE的长.
的中点,AD交BC于点E,AE=4,AB=6,求DE的长.