题目内容
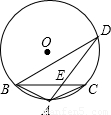
(2008•清远)如图,A,B,C,D是⊙O上的四个点,点A是 的中点,AD交BC于点E,AE=4,AB=6,求DE的长.
的中点,AD交BC于点E,AE=4,AB=6,求DE的长.
【答案】分析:显然可以把要求的线段和已知线段放到两个相似三角形中,根据等弧所对的圆周角相等得到∠ABE=∠D,结合公共角,根据两角对应相等即可证明两个三角形相似.根据相似三角形的性质得到比例式,再进一步计算即可.
解答:解:∵点A是 的中点,
的中点,
∴∠ABE=∠D.又∠BAE=∠DAB,
∴△ABE∽△ADB,
∴ ,即AD=
,即AD=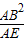 =9,
=9,
则DE=9-4=5.
点评:考查了相似三角形的判定和性质.
解答:解:∵点A是
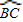 的中点,
的中点,∴∠ABE=∠D.又∠BAE=∠DAB,
∴△ABE∽△ADB,
∴
 ,即AD=
,即AD=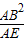 =9,
=9,则DE=9-4=5.
点评:考查了相似三角形的判定和性质.

练习册系列答案
相关题目
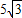 米,若挖掘的速度为2米/小时,几小时后到达B点?
米,若挖掘的速度为2米/小时,几小时后到达B点?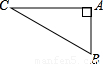
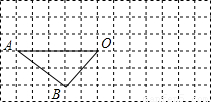
 的中点,AD交BC于点E,AE=4,AB=6,求DE的长.
的中点,AD交BC于点E,AE=4,AB=6,求DE的长.