Question

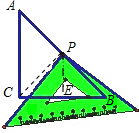
操作与探索：如图，在△ABC中，AC=BC=2，∠C=90°，将一块三角板的直角顶点放在斜边的中点P处，绕点P旋转．设三角板的直角边PM交线段CB于E点，当CE=0，即E点和C点重合时，有PE=PB，△PBE为等腰三角形，此外，当CE等于______时，△PBE为等腰三角形．

Answer 1

∵在△ABC中，AC=BC=2，∠C=90°，
∴AB=

AC2+BC2

=2

2

，
又∵P点为AB的中点，
∴PB=

2

，
①若PE=PB，连接PC，∵PB=PC，∴C、E两点重合，此时CE=0；
②若PB=BE，则CE=BC-BE=2-

2

；
③若PE=BE，此时PE⊥BE，
∵P点为AB的中点，∴E点为BC的中点，
即CE=

1

2

BC=1．
故答案为：1或2-

2

．