Question

【题目】如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高22米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有25米的距离（B，F，C在一条直线上）．

（1）求办公楼AB的高度；
（2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．
（参考数据：sin22°≈ ，cos22°≈ ，tan22≈ ）

Answer 1

【答案】
（1）

解：过点E作EM⊥AB于点M，设AB=x，

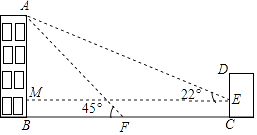
在Rt△ABF中，∵∠AFB=45°，

∴BF=AB=x，

∴BC=BF+FC=x+25．

在Rt△AEM中，

∵∠AEM=22°，AM=AB﹣CE=x﹣2，tan22°= ，即 = ，解得x=20．

∴办公楼AB的高度为20m；

（2）

解：在Rt△AME中，∵cos22°= ，

∴AE= = =48m．

答：A，E之间的距离为48m．

【解析】（1）过点E作EM⊥AB于点M，设AB=x，在Rt△ABF中，由∠AFB=45°可知BF=AB=x，在Rt△AEM中，利用锐角三角函数的定义求出x的值即可；（2）在Rt△AME中，根据cos22°= 可得出结论．