题目内容
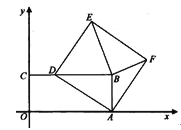
【题目】如图,在平面直角坐标系中,正方形ABCO的边长为3,点O为坐标原点,点A、C分别在x轴、y轴上,点B在第一象限内直线y=kx+1分别与x轴、y轴、线段BC交于点F、D、G,AE⊥FG,下列结论:①△GCD和△FOD的面积比为3:1:②AE的最大长度为![]() :③tan∠FEO=
:③tan∠FEO=![]() ④当DA平分∠EAO时,CG=
④当DA平分∠EAO时,CG=![]() ,其中正确的结论有( )
,其中正确的结论有( )

A. ①②③ B. ②③ C. ②③④ D. ③④
【答案】C
【解析】分析:令x=0,得y=1,得OD=1,由OD=1得CD=2,易证△GCD∽△FOD,从而可得△GCD和△FOD的面积比为4:1,故①错误;由勾股定理和三角形三边关系可得AE的最大长度为![]() ,故②正确;由OD⊥OA,AE⊥DE得A、O、D、E四点共圆,由∠FEO+∠OEA=90°,∠ODA+∠OAD=90°,∠OEA=∠ODA得∠FEO=∠ODA故tan∠FEO=tan∠ODA=
,故②正确;由OD⊥OA,AE⊥DE得A、O、D、E四点共圆,由∠FEO+∠OEA=90°,∠ODA+∠OAD=90°,∠OEA=∠ODA得∠FEO=∠ODA故tan∠FEO=tan∠ODA=![]() ,故③正确;当DA平分∠OAE时,OE=OD=1,设OF=a,延长AE至点H,则OH=DF=
,故③正确;当DA平分∠OAE时,OE=OD=1,设OF=a,延长AE至点H,则OH=DF=![]() ,在Rt△HOA中,HO=1+
,在Rt△HOA中,HO=1+![]() ,OA=3,HA=3+a,HO2+OA2=HA2 解得a=
,OA=3,HA=3+a,HO2+OA2=HA2 解得a=![]() ,故CG=2a=
,故CG=2a=![]() ,所以④正确.
,所以④正确.
详解:令x=0,得y=1,得OD=1,由OD=1得CD=2,易证△GCD∽△FOD,
∴S△GCD:S△FOD=4:1,故①错误;
在Rt△AOE中,AD>AE,所以AE的最大值为AD的长,AD=![]() ,故②正确;
,故②正确;
∵OD⊥OA,AE⊥DE
∴A、O、D、E四点共圆,
∵∠FEO+∠OEA=90°,∠ODA+∠OAD=90°,∠OEA=∠ODA(同弧所对的圆周角相等)
∴∠FEO=∠ODA
∴tan∠FEO=tan∠ODA=![]() ,故③正确;
,故③正确;
当DA平分∠OAE时,OE=OD=1
设OF=a,延长AE至点H,则OH=DF=![]()
在Rt△HOA中,HO=1+![]() ,OA=3,HA=3+a
,OA=3,HA=3+a
HO2+OA2=HA2 解得a=![]()
∴CG=2a=![]() ,故④正确.
,故④正确.
故选C.

 考前必练系列答案
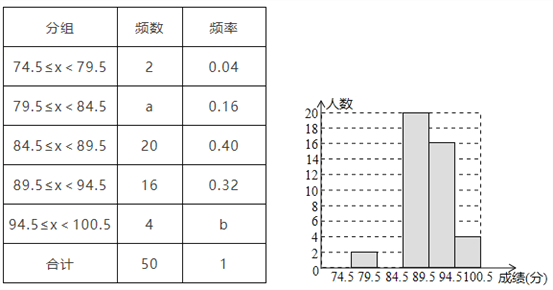
考前必练系列答案【题目】我市某小区开展了“节约用水为环保做贡献”的活动,为了解居民用水情况,在小区随机抽查了10户家庭的月用水量,结果如下表
月用水量(吨) | 8 | 9 | 10 |
户数 | 2 | 6 | 2 |
则关于这10户家庭的月用水量,下列说法错误的是 ( )
A. 方差是4 B. 极差2 C. 平均数是9 D. 众数是9