Question

【题目】用两个全等的等边△ABC和△ACD拼成菱形ABCD．把一个含60°角的三角尺与这个菱形叠合，使三角尺60°角的项点与点A重合，两边分别与AB、AC重合，将三角尺绕点A按逆时针方向旋转．当三角尺的两边分别与菱形的两边BC、CD相交于点E、F时（如图），通过观察或测量BE、CF的长度，你能得出什么结论？并证明你的结论．

Answer 1

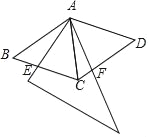
【答案】BE=CF．

【解析】

由于菱形ABCD由等边△ABC和△ACD拼成，根据等边三角形的性质得到AB=AC，∠B=∠CAB=∠ACD=60°，而∠FAE=60°，得到∠BAE=60°﹣∠CAE=∠CAF，根据全等三角形的判定方法易得△BAE≌△CAF，即可得到BE=CF.

结论：BE=CF．

理由：∵菱形ABCD由等边△ABC和△ACD拼成，

∴AB=AC，∠B=∠CAB=∠ACD=60°，

而∠FAE=60°，

∴∠BAE=60°﹣∠CAE=∠CAF，

在△BAE和△CAF中

，

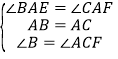∴△BAE≌△CAF，

∴BE=CF.