题目内容
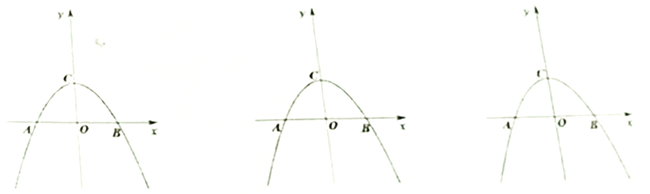
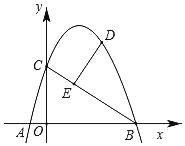
【题目】如图,抛物线y=ax2+bx+c经过A(﹣1,0)、B(4,0)、C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于点E.
(1)求抛物线的函数表达式;
(2)求线段DE长度的最大值.
【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2)最大值是
x+3;(2)最大值是![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得DM,根据相似三角形的判定与性质,可得DE的长,根据二次函数的性质,可得答案.
解:(1)由题意得,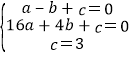 ,
,
解得,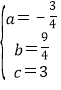 ,
,
抛物线的函数表达式为y=﹣![]() x2+
x2+![]() x+3;
x+3;
(2)过点D作DM⊥x轴交BC于M点,
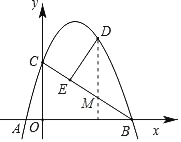
由勾股定理得,BC=![]() =5,
=5,
设直线BC的解析是为y=kx+b,
则![]() ,
,
解得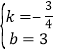 ,
,
∴直线BC的解析是为y=﹣![]() x+3,
x+3,
设点M的坐标为(a,﹣![]() a+3),
a+3),
DM=(﹣![]() a2+
a2+![]() a+3)﹣(﹣
a+3)﹣(﹣![]() a+3)=﹣
a+3)=﹣![]() a2+3a,
a2+3a,
∵∠DME=∠OCB,∠DEM=∠BOC,
∴△DEM∽△BOC,
∴![]() ,即
,即![]() =
=![]() ,
,
解得,DE=![]() DM
DM
∴DE=﹣![]() a2+
a2+![]() a=﹣
a=﹣![]() (a﹣2)2+
(a﹣2)2+![]() ,
,
当a=2时,DE取最大值,最大值是![]() .
.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目