题目内容
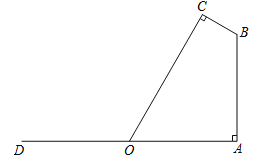
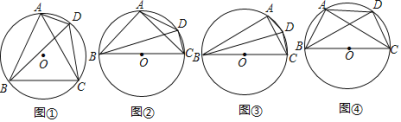
【题目】 如图,已知在![]() 中,
中,![]() ,
,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径作⊙
长为半径作⊙![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若AB=2,求图中阴影部分的面积.

【答案】(1)证明略;(2)![]() .
.
【解析】
(1)连接OD,求出∠OAD=60°,得出等边三角形OAD,求出AD=OA=AC,∠ODA=∠O=60°,求出∠ADC=∠ACD=![]() ∠OAD=30°,求出∠ODC=90°,根据切线的判定得出即可;
∠OAD=30°,求出∠ODC=90°,根据切线的判定得出即可;
(2)求出OD,根据勾股定理求出CD长,分别求出三角形ODC和扇形AOD的面积,相减即可.
(1)证明:连接OD,
∵∠BCA=90°,∠B=30°,
∴∠OAD=∠BAC=60°,
∵OD=OA,
∴△OAD是等边三角形,
∴AD=OA=AC,∠ODA=∠O=60°,
∴∠ADC=∠ACD=![]() ∠OAD=30°,
∠OAD=30°,
∴∠ODC=60°+30°=90°,
即OD⊥DC,
∵OD为半径,
∴CD是⊙O的切线;
(2)解:∵AB=2,∠ACB=90°,∠B=30°,
∴OD=OA=AC=![]() AB=1,
AB=1,
由勾股定理得:CD=![]() ,
,
∴S阴影=S△ODC-S扇形AOD![]() .
.

【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
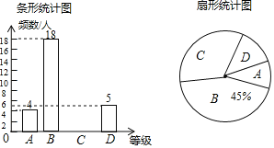
整理上面数据,得到条形统计图:
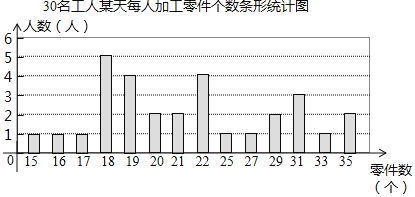
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.