题目内容
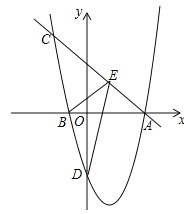
【题目】如图,抛物线![]() (a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)E(﹣2,﹣5);(3)
;(2)E(﹣2,﹣5);(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)把A、B两点的坐标代入,利用待定系数法可求得抛物线的解析式;
(2)当S△ABE=S△ABC时,可知E点和C点的纵坐标相同,可求得E点坐标;
(3)在△CAE中,过E作ED⊥AC于点D,可求得ED和AD的长度,设出点P坐标,过P作PQ⊥x轴于点Q,由条件可知△EDA∽△PQA,利用相似三角形的对应边可得到关于P点坐标的方程,可求得P点坐标.
试题解析:(1)把A、B两点坐标代入解析式![]() ,可得:
,可得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)在![]() 中,令x=0可得y=﹣5,∴C(0,﹣5),∵S△ABE=S△ABC,且E点在x轴下方,∴E点纵坐标和C点纵坐标相同,当y=﹣5时,代入可得
中,令x=0可得y=﹣5,∴C(0,﹣5),∵S△ABE=S△ABC,且E点在x轴下方,∴E点纵坐标和C点纵坐标相同,当y=﹣5时,代入可得![]() ,解得x=﹣2或x=0(舍去),∴E点坐标为(﹣2,﹣5);
,解得x=﹣2或x=0(舍去),∴E点坐标为(﹣2,﹣5);
(3)假设存在满足条件的P点,其坐标为(m,![]() ),如图,连接AP、CE、AE,过E作ED⊥AC于点D,过P作PQ⊥x轴于点Q,则AQ=AO+OQ=5+m,PQ=
),如图,连接AP、CE、AE,过E作ED⊥AC于点D,过P作PQ⊥x轴于点Q,则AQ=AO+OQ=5+m,PQ=![]() ,在Rt△AOC中,OA=OC=5,则AC=
,在Rt△AOC中,OA=OC=5,则AC=![]() ,∠ACO=∠DCE=45°,由(2)可得EC=2,在Rt△EDC中,可得DE=DC=
,∠ACO=∠DCE=45°,由(2)可得EC=2,在Rt△EDC中,可得DE=DC=![]() ,∴AD=AC﹣DC=
,∴AD=AC﹣DC=![]() =
=![]() .当∠BAP=∠CAE时,则△EDA∽△PQA,∴
.当∠BAP=∠CAE时,则△EDA∽△PQA,∴![]() ,即
,即 ,∴
,∴![]() 或
或![]() ;
;
①当![]() 时,整理可得
时,整理可得![]() ,解得m=
,解得m=![]() 或m=﹣5(与A点重合,舍去);
或m=﹣5(与A点重合,舍去);
②当![]() 时,整理可得
时,整理可得![]() ,解得m=
,解得m=![]() 或m=﹣5(与A点重合,舍去),∴存在满足条件的点P,其横坐标为
或m=﹣5(与A点重合,舍去),∴存在满足条件的点P,其横坐标为![]() 或
或![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案