题目内容
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上. 
(1)图中的全等三角形有;
(2)从你找到的全等三角形中选出其中一对加以证明.
【答案】
(1)△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE
(2)解:理由如下:
∵D是BC的中点,
∴BD=CD,
在△ABD和△ACD中,
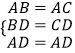 ,
,
∴△ABD≌△ACD(SSS);
∴∠BAE=∠CAE,
在△ABE和△ACE中,
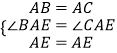 ,
,
∴△ABE≌△ACE(SAS);
∴BE=CE,
在△BDE和△CDE中,
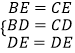 ,
,
∴△BDE≌△CDE(SSS).
故答案为:△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE.
【解析】解:(1)图中的全等三角形有:△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE;
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)).

练习册系列答案
相关题目