题目内容
已知，Rt△ABC中，∠C=90°，斜边AB上的高为5cm，以点C为圆心，4.8为半径的圆与该直线AB的交点个数为
- A.0个
- B.1个
- C.2个
- D.3个
A
分析：根据直线和圆的位置关系与数量之间的联系进行判断．若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．
解答：∵d=5cm＞r=4.8cm，
∴圆与该直线AB的位置关系是相离，交点个数为0，
故选A．
点评：考查了直线和圆的位置关系与数量之间的联系，难度一般，关键是掌握d与r的大小关系所决定的直线与圆的位置关系．
分析：根据直线和圆的位置关系与数量之间的联系进行判断．若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．
解答：∵d=5cm＞r=4.8cm，
∴圆与该直线AB的位置关系是相离，交点个数为0，
故选A．
点评：考查了直线和圆的位置关系与数量之间的联系，难度一般，关键是掌握d与r的大小关系所决定的直线与圆的位置关系．
练习册系列答案
相关题目
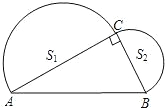如图，已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC、BC为直径作半圆，面积分别记为S1、S2，则S1+S2等于
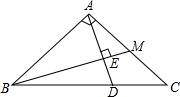如图，已知在Rt△ABC中，∠BAC=90°，AB=AC，M是AC的中点，AD⊥BM于E，交BC于D点．已知在Rt△ABC中，∠C=90°，sinA
，则tanB的值为（ ）
| ||
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
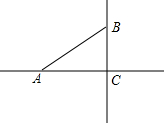如图：已知在Rt△ABC中，∠C=90°，AC=4，BC=3，在直线AC上找点P，使△ABP是等腰三角形，则AP的长度为