题目内容
已知在Rt△ABC中,∠C=90°,sinA
,则tanB的值为( )
| ||
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
分析:先根据sinA=
求出∠A的度数,再根据三角形内角和定理求出∠B的度数,由特殊角的三角函数值即可求出tanB的值.
| ||
| 2 |
解答:解:∵Rt△ABC中,∠C=90°,sinA=
,
∴∠A=45°,
∴∠B=180°-∠A-∠C=180°-90°-45°=45°.
∵tan45°=1,
∴tanB=tan45°=1.
故选A.
| ||
| 2 |
∴∠A=45°,
∴∠B=180°-∠A-∠C=180°-90°-45°=45°.
∵tan45°=1,
∴tanB=tan45°=1.
故选A.
点评:本题考查的是特殊角的三角函数及三角形内角和定理,熟记各特殊角度的三角函数值是解答此题的关键,

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
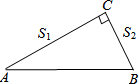 如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( ) (1)已知在Rt△ABC中,∠C=90°,sinA=
(1)已知在Rt△ABC中,∠C=90°,sinA=