题目内容
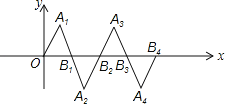
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是 .
【答案】(4n+1,![]() )
)
【解析】
试题分析:首先根据△OA1B1是边长为2的等边三角形,可得A1的坐标为(1,![]() ),B1的坐标为(2,0);然后根据中心对称的性质,分别求出点A2、A3、A4的坐标各是多少;最后总结出An的坐标的规律,求出A2n+1的坐标是多少即可.
),B1的坐标为(2,0);然后根据中心对称的性质,分别求出点A2、A3、A4的坐标各是多少;最后总结出An的坐标的规律,求出A2n+1的坐标是多少即可.
解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,![]() ),B1的坐标为(2,0),
),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣![]() =﹣
=﹣![]() ,
,
∴点A2的坐标是(3,﹣![]() ),
),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣![]() )=
)=![]() ,
,
∴点A3的坐标是(5,![]() ),
),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣![]() =﹣
=﹣![]() ,
,
∴点A4的坐标是(7,﹣![]() ),
),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,
∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是![]() ,当n为偶数时,An的纵坐标是﹣
,当n为偶数时,An的纵坐标是﹣![]() ,
,
∴顶点A2n+1的纵坐标是![]() ,
,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,![]() ).
).
故答案为:(4n+1,![]() ).
).

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
