题目内容
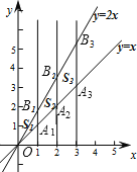
【题目】 如图，直线l1⊥x轴于点（1，0），直线l2⊥x轴于点（2，0），直线l3⊥x轴于点（3，0），…，直线ln⊥x轴于点（n，0）．函数y=x的图象与直线l1，l2，l3，…，ln分别交于点A1，A2，A3，…，An；函数y=2x的图象与直线l1，l2，l3，…，ln分别交于点B1，B2，B3，…，Bn．如果△OA1B1的面积记作S1，四边形A1A2B2B1的面积记作S2，四边形A2A3B3B2的面积记作S3，…，四边形An-1AnBnBn-1的面积记作Sn，那么S2019=______．
【答案】
【解析】
先结合图形确定
的长度规律及图形形状为梯形的规律，再根据所得规律将具体值代入梯形面积公式即得．
解：由题意可得：当
时，
，
∴
∴
，
∵直线l1⊥x轴，直线l2⊥x轴，直线l3⊥x轴，
，直线ln⊥x轴
∴l1∥l2∥l3∥∥ln
∴当
时四边形An-1AnBnBn-1是梯形
∵平行线间距离处处相等，所以梯形An-1AnBnBn-1的高为1
∴
∴
故答案为：
．
练习册系列答案
53随堂测系列答案
相关题目
