Question

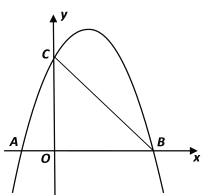
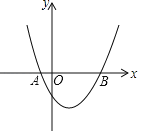
【题目】如图，二次函数y=ax2+bx+c过点A(﹣1，0)，B(3，0)和点C(4，5)．

(1)求该二次函数的表达式及最小值．

(2)点P(m，n)是该二次函数图象上一点．

①当m=﹣4时，求n的值；

②已知点P到y轴的距离不大于4，请根据图象直接写出n的取值范围．

Answer 1

【答案】(1) y=x2﹣2x﹣3，-4；(2)①21；②﹣4≤n≤21

【解析】

（1）根据题意，设出二次函数交点式，点C坐标代入求出a值，把二次函数化成顶点式即可得到最小值；

（2）①m=-4，直接代入二次函数表达式，即可求出n的值；

②由点P到y轴的距离不大于4，得出﹣4≤m≤4，结合二次函数图象可知，m=1时，n取最小值，m=-4时，n取最大值，代入二次函数的表达式计算即可．

解：(1)根据题意，设二次函数表达式为，，点C代入，

得，

∴a=1，

∴函数表达式为y=x2﹣2x﹣3，

化为顶点式得：，

∴x=1时，函数值最小y=-4，

故答案为：；-4；

(2)①当m=﹣4时，n=16+8﹣3=21，

故答案为：21；

②点P到y轴的距离为|m|，

∴|m|≤4，

∴﹣4≤m≤4，

∵y=x2﹣2x﹣3=(x﹣1)2﹣4，

在﹣4≤m≤4时，

当m=1时，有最小值n=-4；当m=-4时，有最大值n=21，

∴﹣4≤n≤21，

故答案为：﹣4≤n≤21．