题目内容
【题目】如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,则下列四个结论: (1) DE=DF; (2) AD上任一点到点C、点B的距离相等; (3) BD=CD,AD⊥BC;(4)∠BDE=∠CDF,其中,正确的有__________个.
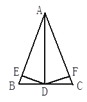
【答案】4
【解析】
根据角平分线上的点到角的两边的距离相等可得DE=DF,判断出(1)正确;根据线段垂直平分线上的点到线段两端点的距离相等判断出(2)正确;根据等腰三角形三线合一的性质判断出(3)正确;根据等腰三角形的性质及三角形的内角和定理,判断出(4)正确.
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,E、F为垂足,
∴DE=DF,(1)正确;
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,BD=CD,
∴线段AD上任一点到点C、点B的距离相等,
∴(2),(3)正确;
∵AB=AC,
∴∠B=∠C;
∵∠BED=∠DFC=90°,
∴∠BDE=∠CDF,(4)正确.
∴正确的结论为:(1)(2)(3)(4).
故答案为:4.

练习册系列答案
相关题目