题目内容
【题目】体育课上，老师为了解初三女学生定点投篮的情况，随机抽取8名女生进行每人4次定点投篮的测试，进球数的统计如图所示．
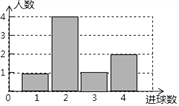
（1）求女生进球数的平均数、中位数；
（2）投球4次，进球3个以上（含3个）为优秀，全校有初三女生400人，从中任选一位女生，求选到的女生投篮成绩为“优秀”等级的的概率？
【答案】（1）2（2）
【解析】试题分析：（1）根据加权平均数的公式求出平均数，然后根据中位数的意义，取中间两个的平均数即可；
（2）先求出“优秀”的概率（百分率），然后用样本的概率估计总体即可.
试题解析：（1）由条形统计图可得，女生进球数的平均数为：（1×1+2×4+1×3+4×2）÷8=2.5（个）；
∵第4，5个数据都是2，则其平均数为：2；
∴女生进球数的中位数为：2，
（2）样本中优秀率为
，根据“样本估计总体”，全校有女生400人，优秀率约为
，故，利用“频率估计概率”，从全校女生中任选一位女生，她的成绩为优秀的概率约为
．
答：全校女生中任选一位女生，她的成绩为优秀的概率约为
．
练习册系列答案
相关题目
【题目】我市某草莓种植农户喜获丰收，共收获草莓2000kg．经市场调查，可采用批发、零售两种销售方式，这两种销售方式每kg草莓的利润如下表：
销售方式 | 批发 | 零售 |
利润（元/kg） | 6 | 12 |
设按计划全部售出后的总利润为y元，其中批发量为xkg．
（1）求y与x之间的函数关系式；
（2）若零售量不超过批发量的4倍，求该农户按计划全部售完后获得的最大利润．
