题目内容
如图，已知直线AB经过⊙O上的点C，并且OA=OB，CA=CB，那么直线AB是⊙O的切线吗？为什么？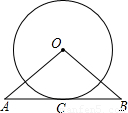
【答案】分析：连接OC，根据等腰三角形的性质，可得OC⊥AB，因为C是圆上一点，即可得AB是⊙O的切线．
解答：
解：直线AB是O的切线，
理由是：连接OC；
∵OA=OB，CA=CB，（等腰三角形三线合一）
∴OC⊥AB，
∴AB是⊙O的切线．
点评：本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．
解答：
解：直线AB是O的切线，理由是：连接OC；
∵OA=OB，CA=CB，（等腰三角形三线合一）
∴OC⊥AB，
∴AB是⊙O的切线．
点评：本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．
练习册系列答案
相关题目
小汽车的速度是大货车速度的2倍，两车在匀速行驶过程中的最近距离是多少？
=1.732）
小汽车的速度是大货车速度的2倍，两车在匀速行驶过程中的最近距离是多少？
=1.732）
AB∥CD和EF∥AB得到。
