题目内容
【题目】在平面直角坐标系xOy中,反比例函数![]() 的图象过点A(1,6).
的图象过点A(1,6).
(1)求反比例函数的表达式;
(2)过点A的直线与反比例函数 ![]() 图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
【答案】(1)y=![]() ;(2)P(﹣1,0).
;(2)P(﹣1,0).
【解析】
试题(1)把A点代入,根据待定系数法即可求得;
(2)作AC⊥x轴于C,BD⊥x轴于D,通过证得△APC∽△BPD,得出![]() =
=![]() =2,求得B的纵坐标,代入解析式求得坐标,然后根据待定系数法求得直线AB的解析式,令y=0,即可求得P的坐标.
=2,求得B的纵坐标,代入解析式求得坐标,然后根据待定系数法求得直线AB的解析式,令y=0,即可求得P的坐标.
解:(1)∵反比例函数y=![]() 的图象过点A(1,6),
的图象过点A(1,6),
∴k=1×6=6,
∴反比例函数的表达式为:y=![]() ;
;
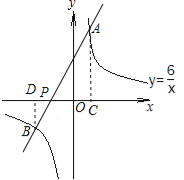
(2)作AC⊥x轴于C,BD⊥x轴于D,
∵AC∥BD,
∴△APC∽△BPD,
∴![]() =
=![]() ,
,
∵AP=2PB,
∴AC=2BD,
∵AC=6,
∴BD=3,
∴B的纵坐标为﹣3,
代入y=![]() 得,﹣3=
得,﹣3=![]() ,解得x=﹣2,
,解得x=﹣2,
∴B(﹣2,﹣3),
设直线AB的解析式为y=kx+b,
∴![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=3x+3,
令y=0,则求得x=﹣1,
∴P(﹣1,0).

练习册系列答案
相关题目
【题目】“滴滴出行”改变了传统打车方式,最大化节省了司机与乘客双方的资源与时间.该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元
元![]() 公里计算,耗时费按
公里计算,耗时费按![]() 元
元![]() 分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:
分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:

平均速度(公里/时) | 里程数(公里) | 车费(元) | |
甲乘客 |
|
|
|
乙乘客 |
|
|
|
(1)求![]() ,
,![]() 的值;
的值;
(2)如果你采用“滴滴出行”的打车方式,保持平均车速![]() 公里
公里![]() 时,行驶了
时,行驶了![]() 公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.
公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.