题目内容
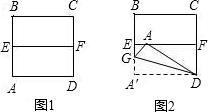
如图所示，在矩形ABCD中，AB=16，BC=8，将矩形沿对角线AC折叠，点D落在E点处，且CE与AB交于点F，则AF的长度为（ ）
| A．6 | B．8 | C．10 | D．12 |
∵在矩形ABCD中，AB=16，BC=8，
∴CD=AB=16，AB∥CD，∠B=90°，
∴∠DCA=∠BAC，
由折叠的性质可得：∠DCA=∠ECA，CE=CD=16，
∴∠BAC=∠ECA，
∴CF=AF，
设AF=x，则CF=x，BF=AB-AF=16-x，
在Rt△BCF中，CF2=BF2+BC2，
即x2=（16-x）2+82，
解得：x=10，
∴AF=10．
故选C．
∴CD=AB=16，AB∥CD，∠B=90°，
∴∠DCA=∠BAC，
由折叠的性质可得：∠DCA=∠ECA，CE=CD=16，
∴∠BAC=∠ECA，
∴CF=AF，
设AF=x，则CF=x，BF=AB-AF=16-x，
在Rt△BCF中，CF2=BF2+BC2，
即x2=（16-x）2+82，
解得：x=10，
∴AF=10．
故选C．
练习册系列答案
53随堂测系列答案
相关题目
