题目内容
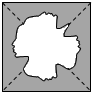
如图,取一张长方形纸片,它的长AB=10cm,宽BC=5
cm,然后以虚线CE(E点在
AD上)为折痕,使D点落在AB边上,则AE=______cm,∠DCE=______.

| 3 |
AD上)为折痕,使D点落在AB边上,则AE=______cm,∠DCE=______.

∵△D′CE是△DCE沿直线CE翻折而成,
∴CD′=AB=CD=10,DE=ED′,
∴在Rt△BCD′中,BD′=
=
=5,
∴AD′=AB-BD′=10-5=5,
设AE=x,则ED′=5
-x,在Rt△AED′中,AE2+AD′2=ED′2,
即x2+52=(5
-x)2,
解得x=
.
∴DE=AD-AE=5
-
=
,
∵tan∠DCE=
=
=
,
∵△CDE是直角三角形,
∴∠DCE=30°.
故答案为:
、30°.
∴CD′=AB=CD=10,DE=ED′,
∴在Rt△BCD′中,BD′=
| CD′2-BC2 |
102-(5
|
∴AD′=AB-BD′=10-5=5,
设AE=x,则ED′=5
| 3 |
即x2+52=(5
| 3 |
解得x=
5
| ||
| 3 |
∴DE=AD-AE=5
| 3 |
5
| ||
| 3 |
10
| ||
| 3 |
∵tan∠DCE=
| DE |
| CD |
| ||||
| 10 |
| ||
| 3 |
∵△CDE是直角三角形,
∴∠DCE=30°.
故答案为:
5
| ||
| 3 |

练习册系列答案
相关题目