题目内容
如图，为了测量笔直的旗杆AB的高度，现将高度为1米的测角仪CD（即CD=1米）与旗杆AB置于同一水平面上，且与旗杆底部相距15米（即CB=15米），测得旗杆顶端A的仰角∠ADE=30°，求旗杆AB的高度．（结果保留根号）
解：在Rt△ADE中，
∵∠AED=90°，∠ADE=30°，DE=15，
∴tan30°=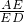
，
∴AE=DEtan30°=15×
=5
，
∴
，
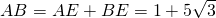答：旗杆AB的高度为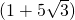
米．
分析：利用tan30°=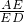，求出AE的长，进而得出AB的长即可得出答案．
点评：此题主要考查了仰角与俯角的应用，利用锐角三角函数关系得出AE的长是解题关键．
∵∠AED=90°，∠ADE=30°，DE=15，
∴tan30°=
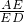，∴AE=DEtan30°=15×
=5，∴
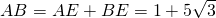，答：旗杆AB的高度为
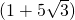米．分析：利用tan30°=
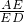，求出AE的长，进而得出AB的长即可得出答案．点评：此题主要考查了仰角与俯角的应用，利用锐角三角函数关系得出AE的长是解题关键．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
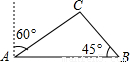
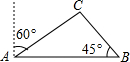去年某省将地处A、B两地的两所大学合并成一所综合大学，为了方便A、B两地师生的交往，学校准备在相距2千米的A、B两地之间修筑一条笔直公路．如图中线段AB，经测量，在A地北偏东60°方向，B地西偏北45°方向的C处有一个半径为0.7千米的公园，问计划修筑的这条公路会不会穿过公园？为什么？
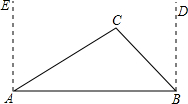不会影响公路的修筑，为什么？（参考数据：
如图，为了测量笔直的旗杆AB的高度，现将高度为1米的测角仪CD（即CD=1米）与旗杆AB置于同一水平面上，且与旗杆底部相距15米（即CB=15米），测得旗杆顶端A的仰角∠ADE=30°，求旗杆AB的高度．（结果保留根号）