题目内容
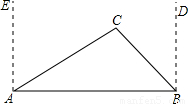
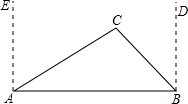
如图,西宁市风景区有2个景点A、B,为了方便游客,风景管理处决定在相距2千米的A、B两景点之间修一笔直公路(即图中的线段AB),经测量,在A点的北偏东60°方向、B点的西偏北45°方向的C处有一个半径为0.7千米的小水潭,问小水潭会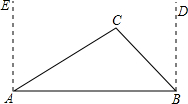 不会影响公路的修筑,为什么?(参考数据:
不会影响公路的修筑,为什么?(参考数据:| 3 |
| 2 |
分析:过C作CD⊥AB于D,求出CF的长就可以判断小水潭会不会影响公路的修筑.
解答: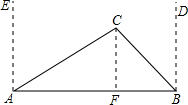 解:过C作CF⊥AB于F(1分),
解:过C作CF⊥AB于F(1分),
设CF=x千米.
∵∠ABC=45°,∠CFB=90°(2分)
∴∠BCF=45°
∴FB=CF=x(3分)
∵∠EAC=60°
∴∠CAF=30°
∴AF=CF•cot30°=
x(3分)
∵AB=2
∴
x+x=2(4分)
∴x=
≈0.732(5分)
∵0.732>0.7
∴小水潭不会影响公路的修筑.(7分)
 解:过C作CF⊥AB于F(1分),
解:过C作CF⊥AB于F(1分),设CF=x千米.
∵∠ABC=45°,∠CFB=90°(2分)
∴∠BCF=45°
∴FB=CF=x(3分)
∵∠EAC=60°
∴∠CAF=30°
∴AF=CF•cot30°=
| 3 |
∵AB=2
∴
| 3 |
∴x=
| 2 | ||
|
∵0.732>0.7
∴小水潭不会影响公路的修筑.(7分)
点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
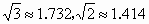 )
)
 不会影响公路的修筑,为什么?(参考数据:
不会影响公路的修筑,为什么?(参考数据: ≈1.732,
≈1.732, ≈1.414)
≈1.414)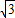 ≈1.732,
≈1.732,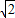 ≈1.414)
≈1.414)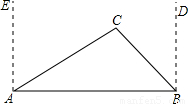
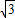 ≈1.732,
≈1.732,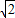 ≈1.414)
≈1.414)