Question

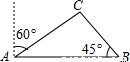
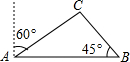去年某省将地处A、B两地的两所大学合并成一所综合大学，为了方便A、B两地师生的交往，学校准备在相距2千米的A、B两地之间修筑一条笔直公路．如图中线段AB，经测量，在A地北偏东60°方向，B地西偏北45°方向的C处有一个半径为0.7千米的公园，问计划修筑的这条公路会不会穿过公园？为什么？

Answer 1

分析：本题要求的实际上是C到AB的距离，过C点作CD⊥AB，CD就是所求的线段，由于CD是条公共直角边，可用CD表示出AD，BD，然后根据AB的长，来求出CD的长．

解答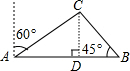：解：过C点作CD⊥AB于D，
由题可知：∠CAD=30°，
设CD=x千米，tan∠CAD=

CD

AD

，
所以AD=

x

3 3

=

3

x，
由CD⊥AB，得到∠CDB=90°，又∠CBD=45°，
所以△CDB为等腰直角三角形，
则BD=CD=x，
∵AB=2，
∴

3

x+x=2，
∴x=

2

3 +1

=

2( 3 -1)

( 3+1)( 3 -1)

=

2( 3 -1)

2

=

3

-1＞0.7．
∴计划修筑的这条公路不会穿过公园．

点评：解直角三角形的应用关键是构建直角三角形，如果有共用直角边的，可以利用公共边来进行求解．