题目内容
【题目】正方形ABCD中，E是AC上一点，EF⊥AB ， EG⊥AD ， AB=6，AE：EC=2：1．求四边形AFEG的面积．
【答案】解答：正方形ABCD中，∠DAB=90°，∠DAC=45°，
又∵∠AFE=∠AGE=90°，
∴四边形AFEG是矩形，∠AEG=90°-∠DAC=45°，
∴∠GAE=∠AEG=45°，
∴GE=AG ，
∴矩形AFEG是正方形，
∵四边形ABCD是正方形，
∴正方形AFEG∽正方形ABCD ，
∴ 
=（ 
）2=（ 
）2= 
，
∴S正方形AFEG= S正方形AFEG= ×62=16．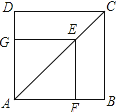
【解析】先证明四边形AFEG是正方形，再由相似的定义得出正方形AFEG∽正方形ABCD ， 最后根据相似多边形的面积比等于相似比的平方进行求解．
【考点精析】掌握相似图形是解答本题的根本，需要知道形状相同，大小不一定相同（放大或缩小）;判定:①平行；②两角相等；③两边对应成比例，夹角相等；④三边对应成比例．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
