题目内容
【题目】在四边形ABCD中,AC、BD交于点E,且∠ACD=∠ADC.
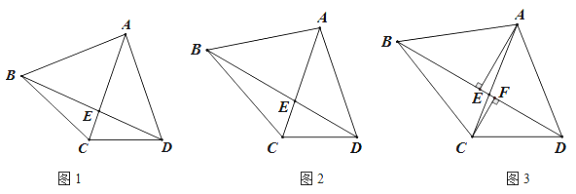
(1)如图1,若AB=AD,求证:∠BAC=2∠BDC;
(2)如图2,在(1)的条件下,若∠BDC=30°,求证:BC=AC.
(3)如图3,若BC=AD,∠BDC=30°,过A作AE⊥BD于E,过C作CF⊥BD于F, 且EF:BE=2:11,DF=9,求BD的长.
【答案】(1)证明见解析;
(2)证明见解析;
(3)BD的长为22.
【解析】试题分析:(1)△ABC和△BCD中,理由三角形内角和定理及等角对等边进行等量代换即可;(2)先由等角对等边、等量代换得出△ABC是等腰三角形,再由∠BDC=30°,∠BAC=2∠BDC得出△ABC是等边三角形,即可得出结果;(3)由已知可得AB=AD,由等腰三角形的性质即可求得.
试题解析:(1)
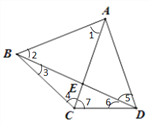
在△ABC中,∠1+∠2+∠3+∠4=180°,
在△BCD中,∠3+∠4+∠6+∠7=180°,
∴∠1+∠2=∠6+∠7,
∵∠ACD=∠ADC,即∠7=∠5+∠6,
∴∠1+∠2=∠6+∠5+∠6,
∵AB=AD,
∴∠2=∠5,
∴∠1+∠5=∠6+∠5+∠6,
∴∠1=2∠6,
即∠BAC=2∠BDC.
(2)∵∠ACD=∠ADC,
∴AC=AD,
∵AB=AD,
∴AC=AB,
∴△ABC是等腰三角形,
∵∠BDC=30°,
∴∠BAC=2∠BDC=60°,
△ABC是等边三角形,
∴BC=AC.
(3)由题可知AB=AD,
∵AE⊥BD,
∴BE=DE.
设EF=2x,BE=11x,
则2x+9=11x,x=1,
∴BD=13+9=22.

练习册系列答案
相关题目
