题目内容
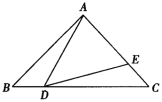
【题目】已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B, C点重合),∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当△ADE是等腰三角形时,请直接写出AE的长.
【答案】(1)证明见解析;(2)y=x2-x+1=(x-![]() )2+
)2+![]() ;(3)AE的长为2-
;(3)AE的长为2-![]() 或
或 ![]() .
.
【解析】
(1)根据等腰直角三角形的性质及三角形内角与外角的关系,易证△ABD∽△DCE.
(2)由△ABD∽△DCE,对应边成比例及等腰直角三角形的性质可求出y与x的函数关系式;
(3)当△ADE是等腰三角形时,因为三角形的腰和底不明确,所以应分AD=DE,AE=DE,AD=AE三种情况讨论求出满足题意的AE的长即可.
(1)证明:
∵∠BAC=90°,AB=AC
∴∠B=∠C=∠ADE=45°
∵∠ADC=∠B+∠BAD=∠ADE+∠CDE
∴∠BAD=∠CDE
∴△ABD∽△DCE;
(2)由(1)得△ABD∽△DCE,
∴![]() =
=![]() ,
,
∵∠BAC=90°,AB=AC=1,
∴BC=![]() ,CD=
,CD=![]() -x,EC=1-y,
-x,EC=1-y,
∴![]() =
=![]() ,
,
∴y=x2-x+1=(x-![]() )2+
)2+![]() ;
;
(3)当AD=DE时,△ABD≌△CDE,
∴BD=CE,
∴x=1-y,即 ![]() x-x2=x,
x-x2=x,
∵x≠0,
∴等式左右两边同时除以x得:x=![]() -1
-1
∴AE=1-x=2-![]() ,
,
当AE=DE时,DE⊥AC,此时D是BC中点,E也是AC的中点,
所以,AE=![]() ;
;
当AD=AE时,∠DAE=90°,D与B重合,不合题意;
综上,在AC上存在点E,使△ADE是等腰三角形,
AE的长为2-![]() 或
或 ![]() .
.

练习册系列答案
相关题目