题目内容
(2012•徐汇区一模)如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,AB=10,tanA=
,点P是CE延长线上的一动点,过点P作PQ⊥CB,交CB延长线于点Q,设EP=x,BQ=y.
(1)求y关于x的函数关系式及定义域;
(2)连接PB,当PB平分∠CPQ时,求PE的长;
(3)过点B作BF⊥AB交PQ于F,当△BEF和△QBF相似时,求x的值.
| 4 | 3 |
(1)求y关于x的函数关系式及定义域;
(2)连接PB,当PB平分∠CPQ时,求PE的长;
(3)过点B作BF⊥AB交PQ于F,当△BEF和△QBF相似时,求x的值.

分析:(1)利用tanA=
,以及AB=10,即可求出BC,AC,再利用△PCQ∽△ABC,利用相似三角形的性质求出y与x的关系式即可;
(2)利用PB平分∠CPQ,BQ⊥PQ,垂足为Q.得出BM=BQ=y,进而求出x即可;
(3)分两种情况:①当∠FEB=∠A时,②当∠FEB=∠ABC时,分别求出即可.
| BC |
| AC |
(2)利用PB平分∠CPQ,BQ⊥PQ,垂足为Q.得出BM=BQ=y,进而求出x即可;
(3)分两种情况:①当∠FEB=∠A时,②当∠FEB=∠ABC时,分别求出即可.
解答:解:(1)在Rt△ABC中,∠ACB=90°,
∵tanA=
=
,AB=10,
∴BC=8,AC=6,
∵CE是斜边AB上的中线,
∴CE=BE=
AB=5,
∴∠PCB=∠ABC,
∵∠PQC=∠ACB=90°,
∴△PCQ∽△ABC,
∴
=
=
,
即
=
,
∴y=
x-4,定义域为x>5.

(2)过点B作BM⊥PC,垂足为M.
∵PB平分∠CPQ,BQ⊥PQ,垂足为Q.
∴BM=BQ=y,
∵tanA=
=
,
设AC=3x,则BC=4x,AB=5x,
∴sin∠MCB=
=
=
,
∴BM=
BC=
×8=
,
∴
x-4=
,
∴x=11,
(3)∵∠Q=∠ACB=90°,∠QBF=∠A,
∴△BQF∽△ABC,
当△BEF和△QBF相似时,
可得△BEF和△ABC也相似.
分两种情况:
①当∠FEB=∠A时,
在Rt△FBE中,∠FBE=90°,BE=5,BF=
y
∴
(
x-4)=
×5,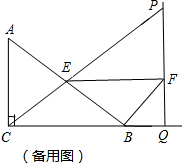
解得x=10;
②当∠FEB=∠ABC时,
在Rt△FBE中,∠FBE=90°,BE=5,BF=
y
∴
(
x-4)=
×5,
解得x=
;
综合①②,x=
或10.
∵tanA=
| BC |
| AC |
| 4 |
| 3 |
∴BC=8,AC=6,
∵CE是斜边AB上的中线,
∴CE=BE=
| 1 |
| 2 |
∴∠PCB=∠ABC,
∵∠PQC=∠ACB=90°,
∴△PCQ∽△ABC,
∴
| CQ |
| PC |
| BC |
| AB |
| 4 |
| 5 |
即
| 8+y |
| 5+x |
| 4 |
| 5 |
∴y=
| 4 |
| 5 |

(2)过点B作BM⊥PC,垂足为M.
∵PB平分∠CPQ,BQ⊥PQ,垂足为Q.
∴BM=BQ=y,
∵tanA=
| 4 |
| 3 |
| BC |
| AC |
设AC=3x,则BC=4x,AB=5x,
∴sin∠MCB=
| BM |
| BC |
| AC |
| AB |
| 3 |
| 5 |
∴BM=
| 3 |
| 5 |
| 3 |
| 5 |
| 24 |
| 5 |
∴
| 4 |
| 5 |
| 24 |
| 5 |
∴x=11,
(3)∵∠Q=∠ACB=90°,∠QBF=∠A,
∴△BQF∽△ABC,
当△BEF和△QBF相似时,
可得△BEF和△ABC也相似.
分两种情况:
①当∠FEB=∠A时,
在Rt△FBE中,∠FBE=90°,BE=5,BF=
| 5 |
| 3 |
∴
| 5 |
| 3 |
| 4 |
| 5 |
| 4 |
| 3 |

解得x=10;
②当∠FEB=∠ABC时,
在Rt△FBE中,∠FBE=90°,BE=5,BF=
| 5 |
| 3 |
∴
| 5 |
| 3 |
| 4 |
| 5 |
| 3 |
| 4 |
解得x=
| 125 |
| 16 |
综合①②,x=
| 125 |
| 16 |
点评:此题主要考查了相似三角形的性质与判定,相似三角形的考查是中考中重点题型,同学们应重点掌握.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 (2012•徐汇区一模)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,如果△ADC和△BDC的周长之比是1:3,则cot∠BCD=
(2012•徐汇区一模)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,如果△ADC和△BDC的周长之比是1:3,则cot∠BCD=