直角三角形ABC中.∠ABC=90°.AC=10.BC=6.AB=8.P是AC上的一个动点.当P在AC上运动时.设PC=x.△ABP 的面积为y. (1)求AC边上的高是多少?(2)求y与x之间的关系式. 题目和参考答案——青夏教育精英家教网—

题目内容

直角三角形ABC中，∠ABC=90°，AC=10，BC=6，AB=8。P是AC上的一个动点，当P在AC上运动时，设PC=x，△ABP 的面积为y.
（1）求AC边上的高是多少？
（2）求y与x之间的关系式。

（1）4.8；（2）y=-2.4x+24

解析试题分析：（1）根据等面积法求解即可；
（2）作PD⊥AB，可得△ADP∽△ABC，根据相似三角形的性质，可用x表示出PD的长，根据S_△_ABP=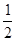AB×PD，代入数值，即可求出y与x之间的关系式．
解：（1）设AC边上的高是x，由题意得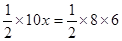

解得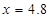
答：AC边上的高是4.8；
（2）作PD⊥AB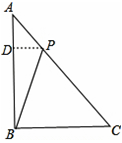

∴△ADP∽△ABC，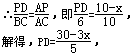

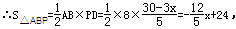
∴y与x之间的关系式为：y=-2.4x+24.
考点：三角形的面积公式，相似三角形的判定和性质
点评：相似三角形的判定和性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.

练习册系列答案

学业测评一卷通小学升学试题汇编系列答案

小学单元综合练习与检测系列答案

实验探究报告练习册系列答案

单元学习体验与评价系列答案

相关题目

如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF=DC，连结并延长交的延长线于点

（1）求证：△ABE∽△DEF；
（2）若正方形的边长为4，求BG的长．

在矩形ABCD中，点P是边AD上的动点，连接BP，线段BP的垂直平分线交边BC于点Q，垂足为点M，连接QP（如图）．已知AD=13，AB=5，设AP=x，BQ=y．

（1）求y关于x的函数解析式，并写出x的取值范围；
（2）当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时，求x的值；
（3）点E在边CD上，过点E作直线QP的垂线，垂足为F，如果EF=EC=4，求x的值．

如图，在矩形ABCD中，点P在边CD上，且与C、D不重合，过点A作AP的垂线与CB的延长线相交于点Q，连接PQ，M为PQ中点．

（1）求证：△ADP∽△ABQ；
（2）若AD=10，AB=20，点P在边CD上运动，设DP=x，BM²=y，求y与x的函数关系式，并求线段BM的最小值；
（3）若AD=10，AB=a，DP=8，随着a的大小的变化，点M的位置也在变化．当点M落在矩形ABCD外部时，求a的取值范围．

（2013年四川绵阳14分）我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心．重心有很多美妙的性质，如关于线段比．面积比就有一些“漂亮”结论，利用这些性质可以解决三角形中的若干问题．请你利用重心的概念完成如下问题：

（1）若O是△ABC的重心（如图1），连结AO并延长交BC于D，证明：；
（2）若AD是△ABC的一条中线（如图2），O是AD上一点，且满足，试判断O是△ABC的重心吗？如果是，请证明；如果不是，请说明理由；
（3）若O是△ABC的重心，过O的一条直线分别与AB、AC相交于G、H（均不与△ABC的顶点重合）（如图3），S_{四边形BCHG}，S_△_AGH分别表示四边形BCHG和△AGH的面积，试探究的最大值．

如图所示，在直角梯形ABCD中，AB为垂直于底边的腰，AD=1，BC=2，AB=3，点E为CD上异于C，D的一个动点，过点E作AB的垂线，垂足为F，△ADE，△AEB，△BCE的面积分别为S₁，S₂，S₃．

（1）设AF=x，试用x表示S₁与S₃的乘积S₁S₃，并求S₁S₃的最大值；
（2）设=t，试用t表示EF的长；
（3）在（2）的条件下，当t为何值时，S₂²=4S₁S₃．