��Ŀ����
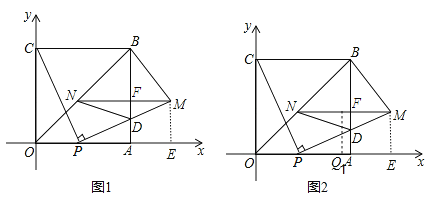
����Ŀ����ͼ�����ı���OABC�DZ߳�Ϊ4�������Σ���PΪOA��������һ�㣨���O��A���غϣ�������CP������P��PM��CP��AB�ڵ�D����PM=CP������M��MN��AO����BO�ڵ�N������ND��BM����OP=t��
��1�����M�����꣨�ú�t�Ĵ���ʽ��ʾ����
��2�����ж��߶�MN�ij����Ƿ����P��λ�õı仯���ı䣿��˵�����ɣ�
��3����tΪ��ֵʱ���ı���BNDM�������С��
��4����x���������ϴ��ڵ�Q��ʹ����QMN�ǵ��������Σ���ֱ��д��������4�����������ĵ�Q�����꣨�ú�t��ʽ�ӱ�ʾ����

���𰸡���1��M��4+t��t������2���߶�MN���Ȳ�������3����t=2ʱ���ı���BNDM�������С����Сֵ6����4��Q1��t+2��0����Q2��4+t��![]() ��0����Q3��4+t+
��0����Q3��4+t+![]() ��0��Q4��t+
��0��Q4��t+![]() ��0����
��0����
��������
�����������1����ME��OA�ڵ�E��Ҫ���M������ֻҪ֤����OPC�ա�EM���ɣ�������Ŀ�е�������֤������������ȫ�ȣ��Ӷ����Եõ���M�����ꣻ
��2�������ж��Ƿ�仯��Ȼ������жϽ����Ŀ�е�����˵�����ɼ��ɽ���⣻
��3��Ҫ��tΪ��ֵʱ���ı���BNDM�������С��ֻҪ�ú�t�Ĵ���ʽ��ʾ���ı��ε������Ȼ��Ϊ����ʽ���ɽ���⣻
��4������д������Ҫ��ĵ�Q�����꣬Ȼ�����д���ĵ������д���Ƶ����̼��ɽ���⣮
�����������1����ͼ1��ʾ����ME��OA�ڵ�E�����MEP=��POC=90�㣬��PM��CP�����CPM=90�㣬���OPC+��MPE=90�㣬���ߡ�OPC+��PCO=90�㣬���MPE=��PCO����PM=CP�����MPE�ա�PCO��AAS������PE=CO=4��ME=PO=t����OE=4+t������M������Ϊ��4+t��t����
��2���߶�MN���Ȳ��䣬���ɣ���OA=AB=4������B��4��4������ֱ��OB�Ľ���ʽΪ��y=x������N��ֱ��OB�ϣ�����N��t��t������MN��OA��M��4+t��t������MN=|��4+t����t|=4����MN�ij��Ȳ��䣻
��3���ɣ�1��֪����MPE=��PCO�����ߡ�DAP=��POC=90�㣬���DAP�ס�POC����![]() ����OP=t��OC=4����AP=4��t����
����OP=t��OC=4����AP=4��t����![]() ����AD=
����AD=![]() ����BD=4��
����BD=4��![]() =
=![]() ����MN��OA��AB��OA����MN��BD����
����MN��OA��AB��OA����MN��BD����![]() =
=![]() MNBD=
MNBD=![]() ��4��
��4��![]() =
=![]() ������t=2ʱ���ı���BNDM�������С����Сֵ6��
������t=2ʱ���ı���BNDM�������С����Сֵ6��
��4����x���������ϴ��ڵ�Q��ʹ����QMN�ǵ��������Σ���ʱ��Q������Ϊ��Q1��t+2��0����Q2��4+t��![]() ��0����Q3��4+t+
��0����Q3��4+t+![]() ��0��Q4��t+
��0��Q4��t+![]() ��0�������ɣ�
��0�������ɣ�
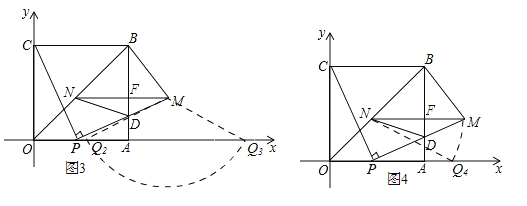
����2����֪��OP=t��0��t��4����MN=PE=4��MN��x�ᣬ��һ���������MNΪ�ױ�ʱ����MN�Ĵ�ֱƽ���ߣ���x��Ľ���ΪQ1����ͼ2��ʾ��PQ1=![]() PE=
PE=![]() MN=2����OQ1=t+2����Q1��t+2��0����
MN=2����OQ1=t+2����Q1��t+2��0����
�ڶ����������ͼ3��ʾ����MNΪ��ʱ����MΪԲ�ģ�MN�ij�Ϊ�뾶������x���ڵ�Q2��Q3������MQ2��MQ3����MQ2=MQ3=4����Q2E=![]() =
=![]() ����OQ2=OE��Q2E=4+t��
����OQ2=OE��Q2E=4+t��![]() ����Q2��4+t��
����Q2��4+t��![]() ��0������OQ3=OE+Q3E=4+t+
��0������OQ3=OE+Q3E=4+t+![]() ����Q3��4+t+
����Q3��4+t+![]() ��0����
��0����
�������������MNΪ��ʱ����NΪԲ�ģ�MN��Ϊ�뾶��Բ����x���ڵ�Q4����0��t��![]() ʱ����ͼ4��ʾ����PQ4=
ʱ����ͼ4��ʾ����PQ4=![]() =
=![]() =
=![]() ����OQ4=OP+PQ4=t+
����OQ4=OP+PQ4=t+![]() ����Q4��t+
����Q4��t+![]() ��0����
��0����

 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�