题目内容
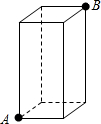 如图,在长、宽都为3cm,高为8cm的长方体纸盒的A处有一粒米粒,一只蚂蚁在B处去觅食,那么它所行的最短路线的长是( )
如图,在长、宽都为3cm,高为8cm的长方体纸盒的A处有一粒米粒,一只蚂蚁在B处去觅食,那么它所行的最短路线的长是( )分析:根据”两点之间线段最短”,将点A和点B所在的两个面进行展开,展开为矩形,则AB为矩形的对角线,即蚂蚁所行的最短路线为AB.
解答: 解:将点A和点B所在的两个面展开,
解:将点A和点B所在的两个面展开,
①矩形的长和宽分别为6cm和8cm,
故矩形对角线长AB=
=10cm;
②矩形的长和宽分别为3cm和11,
故矩形对角线长AB=
=
cm.
即蚂蚁所行的最短路线长是10cm.
故选B.
 解:将点A和点B所在的两个面展开,
解:将点A和点B所在的两个面展开,①矩形的长和宽分别为6cm和8cm,
故矩形对角线长AB=
| 62+82 |
②矩形的长和宽分别为3cm和11,
故矩形对角线长AB=
| 32+112 |
| 130 |
即蚂蚁所行的最短路线长是10cm.
故选B.
点评:本题考查了平面展开-最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题,解本题的关键是将点A和点B所在的面展开,运用勾股定理求出矩形的对角线.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
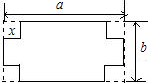 如图,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.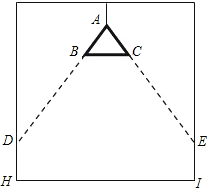 在长、宽都为4m,高为4m的房间正中央的天花板上悬挂一只白炽灯泡,为了集中光线,加上了灯罩如图所示.已知灯罩深8cm,灯泡离地面3m,为了使光线能照在墙壁上的1m高处,问灯罩的直径应为多少?
在长、宽都为4m,高为4m的房间正中央的天花板上悬挂一只白炽灯泡,为了集中光线,加上了灯罩如图所示.已知灯罩深8cm,灯泡离地面3m,为了使光线能照在墙壁上的1m高处,问灯罩的直径应为多少?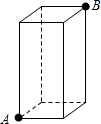 如图,在长、宽都为3cm,高为8cm的长方体纸盒的A处有一粒米粒,一只蚂蚁在B处去觅食,那么它所行的最短路线的长是
如图,在长、宽都为3cm,高为8cm的长方体纸盒的A处有一粒米粒,一只蚂蚁在B处去觅食,那么它所行的最短路线的长是 +8)cm
+8)cm cm
cm