题目内容
（2012•张家港市模拟）如图，以矩形OABC的顶点O为坐标原点，OA所在的直线为x轴，OC所在的直线为y轴，建立直角坐标系．已知OA=3，OC=2，点E是AB的中点，点F在BC上，CF=1，点M、N分别是x轴、y轴上的动点，则四边形MEFN周长的最小值为5+
| 5 |
5+
．| 5 |
分析：由于四边形MEFN中，EF的长度为定值，欲求四边形MEFN周长的最小值，即求其它三边之和的最小值，为此，作点E关于x轴的对称点E′，作点F关于y轴的对称点F′，连接E′F′，分别与x轴、y轴交于点M，N，则线段E′F′的长度就是其它三边之和的最小值．
解答：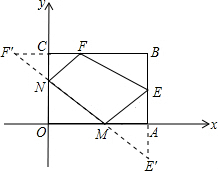
解：如图，作点E关于x轴的对称点E′，作点F关于y轴的对称点F′，连接E′F′，分别与x轴、y轴交于点M，N，则点M，N就是所求点．
∵矩形OABC中，OA=3，OC=2，点E是AB的中点，点F在BC上，CF=1，
∴E′（3，-1），F′（-1，2），NF=NF′，ME=ME′，
∴BF′=4，BE′=3，
∴FN+NM+ME=F′N+NM+ME′=E′F′=
=5，
又∵EF=
=
=
，
∴FN+MN+ME+EF=5+
．
此时四边形MNFE的周长的最小值是5+
．
解：如图，作点E关于x轴的对称点E′，作点F关于y轴的对称点F′，连接E′F′，分别与x轴、y轴交于点M，N，则点M，N就是所求点．∵矩形OABC中，OA=3，OC=2，点E是AB的中点，点F在BC上，CF=1，
∴E′（3，-1），F′（-1，2），NF=NF′，ME=ME′，
∴BF′=4，BE′=3，
∴FN+NM+ME=F′N+NM+ME′=E′F′=
| BE′2+BF′2 |
又∵EF=
| BE2+BF2 |
| 12+22 |
| 5 |
∴FN+MN+ME+EF=5+
| 5 |
此时四边形MNFE的周长的最小值是5+
| 5 |
点评：本题考查了轴对称-最短路线问题，矩形的性质，坐标与图形的性质，难度中等，求线段的和最小的问题基本的解题思路是根据轴对称转化为两点之间的距离的问题．
练习册系列答案
相关题目
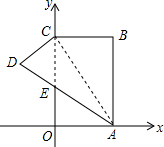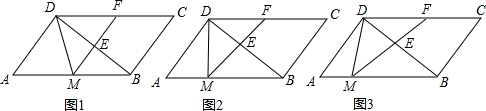
（2012•张家港市模拟）如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，2），将矩形沿对角线AC翻折，点B落在点D的位置，且AD交y轴于点E．那么点D的坐标为（ ）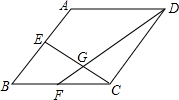
（2012•张家港市模拟）如图，在菱形ABCD中，已知E、F分别是边AB、BC的中点，CE、DF交于点G．若△CGF的面积为2，则菱形ABCD的面积为