题目内容
(2012•张家港市模拟)在平行四边形ABCD中,AB=10,AD=6,AD⊥BD,点M是AB边上的一个动点,ME平分∠DMB,与BD、CD分别交于点E、F.
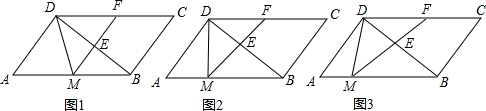
(1)当AM=DM时,证明四边形AMFD是平行四边形;(如图1)
(2)当DM⊥AB时,则ME:EF的值为
(3)当AM为何值时,△DME∽△DBM?(如图3)

(1)当AM=DM时,证明四边形AMFD是平行四边形;(如图1)
(2)当DM⊥AB时,则ME:EF的值为
4:3
4:3
;(如图2)(3)当AM为何值时,△DME∽△DBM?(如图3)
分析:(1)首先利用等边对等角和三角形的外角的性质即可证得∠2=∠3,则AD∥MF,则根据平行四边形的定义即可证得;
(2)首先利用摄影定理求得AM的长,当DM⊥AB时,在直角△ADM中利用勾股定理求得DM的长,则BM即可求得,然后根据△DEF∽△BEM,相似三角形的对应边的比相等即可求解;
(3)当△DME∽△DBM时,易证△EBM是等腰三角形,过E作EH⊥MB于H,则H是BM的中点,根据平行线分线段成比例定理即可求得ED的长,则BH的长度可以求得,进而根据AM=AB-2BH即可求解.
(2)首先利用摄影定理求得AM的长,当DM⊥AB时,在直角△ADM中利用勾股定理求得DM的长,则BM即可求得,然后根据△DEF∽△BEM,相似三角形的对应边的比相等即可求解;
(3)当△DME∽△DBM时,易证△EBM是等腰三角形,过E作EH⊥MB于H,则H是BM的中点,根据平行线分线段成比例定理即可求得ED的长,则BH的长度可以求得,进而根据AM=AB-2BH即可求解.
解答: 证明:(1)∵AM=DM,
证明:(1)∵AM=DM,
∴∠1=∠2,
又∵ME平分∠DMB,
∴∠3=∠4,
又∵∠DMB=∠1+∠2,
∴∠2=∠3,
∴AD∥MF,
又∵AM∥FD,
∴四边形AMFD是平行四边形;
(2)∵在直角△ADM中,DM⊥AB,
∴AD2=AB•AM,
∴AM=
=
=3.6cm,
∴MB=AB-AM=10-3.6=6.4cm,
∴DM=
=
=4.8cm,
∵ME平分∠DMB,即∠DME=∠BME,
又∵AB∥CD,
∴∠BME=∠DFM
∴∠DME=∠DFM
∴DF=DM=4.8cm,
∵AB∥CD,
∴△DEF∽△BEM,
∴ME:EF=MB:DF=6.4:4.8=4:3;
故答案是:4:3.
(3)∵△DME∽△DBM
∴
=
=
,且∠3=∠5,
又∠3=∠4,
∴∠4=∠5,
∴EM=EB,过E作EH⊥MB于H,则H为MB的中点,
∴
=
=
,
又
=
=
∴
=
,
∵DB=8,
∴
=
,则DM=5,
把DM=5代入
=
得:
=
,
∴ED=
,
∴EB=8-
=
,
∴BH=EB•cosB=
×
=
,
∴AM=AB-2BH=10-2×
=
.
 证明:(1)∵AM=DM,
证明:(1)∵AM=DM,∴∠1=∠2,
又∵ME平分∠DMB,
∴∠3=∠4,
又∵∠DMB=∠1+∠2,
∴∠2=∠3,
∴AD∥MF,
又∵AM∥FD,
∴四边形AMFD是平行四边形;
(2)∵在直角△ADM中,DM⊥AB,
∴AD2=AB•AM,
∴AM=
| AD2 |
| AB |
| 36 |
| 10 |
∴MB=AB-AM=10-3.6=6.4cm,
∴DM=
| AD2-AM2 |
| 62-3.62 |
∵ME平分∠DMB,即∠DME=∠BME,
又∵AB∥CD,
∴∠BME=∠DFM
∴∠DME=∠DFM
∴DF=DM=4.8cm,
∵AB∥CD,
∴△DEF∽△BEM,
∴ME:EF=MB:DF=6.4:4.8=4:3;
故答案是:4:3.
(3)∵△DME∽△DBM
∴
| DM |
| DB |
| ME |
| BM |
| ED |
| MD |
又∠3=∠4,
∴∠4=∠5,
∴EM=EB,过E作EH⊥MB于H,则H为MB的中点,

∴
| ME |
| BM |
| EB |
| BM |
| EB |
| 2BH |
又
| EB |
| BH |
| AB |
| BD |
| 5 |
| 4 |
∴
| ME |
| BM |
| 5 |
| 8 |
∵DB=8,
∴
| DM |
| 8 |
| 5 |
| 8 |
把DM=5代入
| DM |
| DB |
| ED |
| MD |
| 5 |
| 8 |
| ED |
| 5 |
∴ED=
| 25 |
| 8 |
∴EB=8-
| 25 |
| 8 |
| 39 |
| 8 |
∴BH=EB•cosB=
| 39 |
| 8 |
| 4 |
| 5 |
| 39 |
| 10 |
∴AM=AB-2BH=10-2×
| 39 |
| 10 |
| 11 |
| 5 |
点评:本题考查了平行四边形的性质,相似三角形的判定与性质,正确求得DM的长度是关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
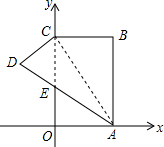 (2012•张家港市模拟)如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,2),将矩形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E.那么点D的坐标为( )
(2012•张家港市模拟)如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,2),将矩形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E.那么点D的坐标为( )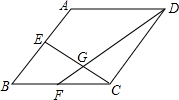 (2012•张家港市模拟)如图,在菱形ABCD中,已知E、F分别是边AB、BC的中点,CE、DF交于点G.若△CGF的面积为2,则菱形ABCD的面积为
(2012•张家港市模拟)如图,在菱形ABCD中,已知E、F分别是边AB、BC的中点,CE、DF交于点G.若△CGF的面积为2,则菱形ABCD的面积为