题目内容
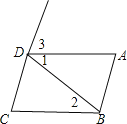
【题目】如图1，在正方形ABCD中，E，F，G，H分别为边AB，BC，CD，DA上的点，HA=EB=FC=GD，连接EG，FH，交点为O．
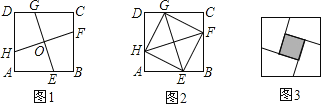
（1）如图2，连接EF，FG，GH，HE，试判断四边形EFGH的形状，并证明你的结论；
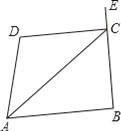
（2）将正方形ABCD沿线段EG，HF剪开，再把得到的四个四边形按图3的方式拼接成一个四边形．若正方形ABCD的边长为3cm，HA=EB=FC=GD=1cm，则图3中阴影部分的面积为 cm2．
【答案】（1）四边形EFGH是正方形．证明见解析；（2）1.
【解析】
试题分析：（1）先证明△AEH≌△BFE≌△CGF≌△DHG，可得出四边形GHEF是菱形，再根据全等三角形角之间的关系，又可得出菱形的一个角是直角，那么就可得出四边形GHEF是正方形．
（2）根据已知条件，可以知道重新拼成的四边形是正方形（因为正方形GHEF的对角线翻到了外边，做了新拼成的正方形的边长），利用勾股定理求出GF和GO、FO的长，所的面积是10减去4个四边形GOFC的面积就是阴影部分的面积．
解：（1）四边形EFGH是正方形．
证明：∵四边形ABCD是正方形，
∴∠A=∠B=∠C=∠D=90°，AB=BC=CD=DA，
∵HA=EB=FC=GD，
∴AE=BF=CG=DH，
∴△AEH≌△BFE≌△CGF≌△DHG，
∴EF=FG=GH=HE，
∴四边形EFGH是菱形，
∵△DHG≌△AEH，
∴∠DHG=∠AEH，
∵∠AEH+∠AHE=90°，
∴∠DHG+∠AHE=90°，
∴∠GHE=90°，
∴四边形EFGH是正方形．
（2）∵HA=EB=FC=GD=1，AB=BC=CD=AD=3，
∴GF=EF=EH=GH=
，
∵由（1）知，四边形EFGH是正方形，
∴GO=OF，∠GOF=90°，
由勾股定理得：GO=OF=
，
∵S四边形FCGO=
×1×2+××
=
，
∴S阴影=
﹣S四边形FCGO×4=10﹣9=1．
